第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
6. (2024 镇江一模)如图,点$A$,$O$在网格中小正方形的顶点处,每个小方格的边长为$1$,该网格中有两个格点(小正方形的顶点)$B$,$C$,使点$O为\triangle ABC$的外心,则$BC$的长度是(
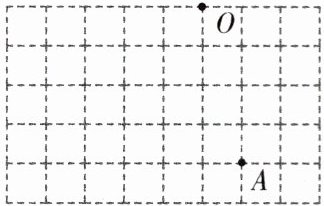
A.$3\sqrt{2}$
B.$2\sqrt{5}$
C.$4$
D.$\sqrt{17}$
C
)
A.$3\sqrt{2}$
B.$2\sqrt{5}$
C.$4$
D.$\sqrt{17}$
答案:
C
1. 直线和圆的位置关系:相交,即直线和圆有两个公共点;相切,即直线和圆只有一个公共点;相离,即直线和圆没有公共点.
2. 设$\odot O$的半径为$r$,圆心$O$到直线$l$的距离为$d$,则有:直线$l$和圆相交$\Leftrightarrow d$
注意:直线与圆的位置关系,决定了圆心到直线的距离$d$与圆的半径$r$的数量关系,反之,亦然.
探究 直线与圆的位置关系
2. 设$\odot O$的半径为$r$,圆心$O$到直线$l$的距离为$d$,则有:直线$l$和圆相交$\Leftrightarrow d$
$ \lt$
$r$;直线$l$和圆相切$\Leftrightarrow d$$=$
$r$;直线$l$和圆相离$\Leftrightarrow d$$\gt$
$r$.注意:直线与圆的位置关系,决定了圆心到直线的距离$d$与圆的半径$r$的数量关系,反之,亦然.
探究 直线与圆的位置关系
答案:
$ \lt$,$=$,$\gt$
例 在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$BC= 3$,$AC= 4$,以点$C$为圆心,$2.5$为半径画圆,则$\odot C与直线AB$的位置关系是(
A.相交
B.相切
C.相离
D.不能确定
名师导引 判断直线与圆的位置关系,可转化为判断圆心到直线的距离与圆的半径之间的数量关系,由数量关系即可确定位置关系.
A
)A.相交
B.相切
C.相离
D.不能确定
名师导引 判断直线与圆的位置关系,可转化为判断圆心到直线的距离与圆的半径之间的数量关系,由数量关系即可确定位置关系.
答案:
A
变式训练 $\odot O的半径为3$,点$O到直线l上的距离为d$,若直线$l与\odot O$没有公共点,则$d$的取值范围是(
A.$d<3$
B.$d>3$
C.$d= 3$
D.$d\leqslant 3$
B
)A.$d<3$
B.$d>3$
C.$d= 3$
D.$d\leqslant 3$
答案:
B
1. (2024巴蜀阶段练习)已知$\odot O的半径为3$,圆心$O到直线l的距离为2$,则$\odot O与直线l$的位置关系是(
A.相切
B.相交
C.相离
D.相交或相离
B
)A.相切
B.相交
C.相离
D.相交或相离
答案:
B
2. (2024巴南区期末)已知$\odot O的半径为3$,圆心$O到直线l的距离为4$,则直线$l与\odot O$的公共点的个数为(
A.$0$
B.$1$
C.$2$
D.以上都不对
A
)A.$0$
B.$1$
C.$2$
D.以上都不对
答案:
A
3. (2024广州阶段练习)已知圆的半径为$6.5\mathrm{cm}$,如果圆心到直线$l的距离为5.5\mathrm{cm}$,那么直线$l$和这个圆的位置关系是(
A.相交
B.相切
C.相离
D.相交或相离
A
)A.相交
B.相切
C.相离
D.相交或相离
答案:
A
查看更多完整答案,请扫码查看


