第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
3. (2023 商洛期末)某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了 10 条航线,则这个航空公司共有
5
个飞机场。
答案:
5
4. (2023 朝阳县期末)某生物兴趣小组的学生将自己收集的标本向本组其他成员各赠送一个,全组共互赠了 72 个,则该兴趣小组共有
9
名学生。
答案:
9
5. 某地出现流感,开始有 2 人患上流感,经过两轮传染后,共有 72 人患上流感。
(1)每轮传染中,平均一个人传染了多少个人?
(2)如果第三轮传染仍保持相同的传染速度,那么经三轮传染后共有多少人患上流感?
(1)每轮传染中,平均一个人传染了多少个人?
(2)如果第三轮传染仍保持相同的传染速度,那么经三轮传染后共有多少人患上流感?
答案:
(1)设每轮传染中平均一个人传染了$x$个人。
根据题意,得$2(1+x)^2=72$,
两边同除以2:$(1+x)^2=36$,
开平方:$1+x=\pm6$,
解得$x_1=5$,$x_2=-7$(不合题意,舍去)。
(2)第三轮新增患病人数为$72×5=360$,
三轮后总人数为$72+360=432$。
(1)5;
(2)432
(1)设每轮传染中平均一个人传染了$x$个人。
根据题意,得$2(1+x)^2=72$,
两边同除以2:$(1+x)^2=36$,
开平方:$1+x=\pm6$,
解得$x_1=5$,$x_2=-7$(不合题意,舍去)。
(2)第三轮新增患病人数为$72×5=360$,
三轮后总人数为$72+360=432$。
(1)5;
(2)432
6. 某生物实验室需要培养一种细胞。现有 60 个细胞,每个细胞经一轮培养后一次可分裂出的细胞数目相同,则经过两轮培养后,细胞总数为 240 个。
(1)每轮分裂中,平均每个细胞可分裂出多少个细胞?
(2)按照这样的分裂速度,经过三轮培养后共有多少个细胞?
(1)每轮分裂中,平均每个细胞可分裂出多少个细胞?
(2)按照这样的分裂速度,经过三轮培养后共有多少个细胞?
答案:
(1)设每轮分裂中,平均每个细胞可分裂出$x$个细胞。
根据题意,得$60(1+x)^2=240$
化简得$(1+x)^2=4$
开平方得$1+x=\pm2$
解得$x_1=1$,$x_2=-3$(不合题意,舍去)
(2)经过三轮培养后细胞总数为$60(1+1)^3=60×8=480$
(1)1;
(2)480
(1)设每轮分裂中,平均每个细胞可分裂出$x$个细胞。
根据题意,得$60(1+x)^2=240$
化简得$(1+x)^2=4$
开平方得$1+x=\pm2$
解得$x_1=1$,$x_2=-3$(不合题意,舍去)
(2)经过三轮培养后细胞总数为$60(1+1)^3=60×8=480$
(1)1;
(2)480
7. (探究与实践)(2023 盐田期中)某校要举办足球赛,若有 5 支球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
模型构建
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题。为解决上述问题,我们构建如下数学模型:
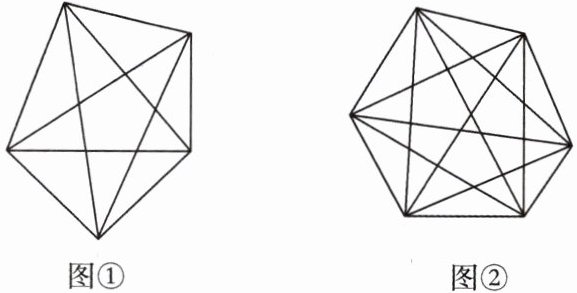
(1)如图①,我们可以在平面内画出 5 个点(任意 3 个点都不在同一条直线上),其中每个点各代表一支足球队,两支足球队之间比赛一场就用一条线段把它们连接起来。由于每支足球队都要与其他各队比赛一场,即每个点与另外 4 个点都可连成一条线段,这样一共连成 $ 5 × 4 $ 条线段,而每两个点之间的线段都重复计算了一次,实际只有 $ \frac{5 × 4}{2} $ 条线段,所以该校一共要安排 10 场比赛。
(2)若学校有 6 支足球队进行单循环比赛,借助图②,可知该校一共要安排____
(3)根据以上规律,若学校有 $ n $ 支足球队进行单循环比赛,则一共要安排____
实际应用
(4)老师为了让数学兴趣班的同学互相认识,请班上 35 位同学每两个人都相互握一次手,全班同学总共握手____
拓展提高
(5)往返于深圳和潮汕的同一辆高速列车,中途经惠州、陆丰、普宁、潮阳 4 个车站(每种车票票面都印有上车车站名称与下车车站名称),请问在这段线路上往返行车,要准备多少种车票?
模型构建
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题。为解决上述问题,我们构建如下数学模型:
(1)如图①,我们可以在平面内画出 5 个点(任意 3 个点都不在同一条直线上),其中每个点各代表一支足球队,两支足球队之间比赛一场就用一条线段把它们连接起来。由于每支足球队都要与其他各队比赛一场,即每个点与另外 4 个点都可连成一条线段,这样一共连成 $ 5 × 4 $ 条线段,而每两个点之间的线段都重复计算了一次,实际只有 $ \frac{5 × 4}{2} $ 条线段,所以该校一共要安排 10 场比赛。
(2)若学校有 6 支足球队进行单循环比赛,借助图②,可知该校一共要安排____
15
场比赛。(3)根据以上规律,若学校有 $ n $ 支足球队进行单循环比赛,则一共要安排____
$\frac{n(n - 1)}{2}$
场比赛。实际应用
(4)老师为了让数学兴趣班的同学互相认识,请班上 35 位同学每两个人都相互握一次手,全班同学总共握手____
595
次。拓展提高
(5)往返于深圳和潮汕的同一辆高速列车,中途经惠州、陆丰、普宁、潮阳 4 个车站(每种车票票面都印有上车车站名称与下车车站名称),请问在这段线路上往返行车,要准备多少种车票?
30

答案:
(2)$ \frac{6 × 5}{2} = 15 $
答案:15
(3)$ \frac{n(n - 1)}{2} $
答案:$ \frac{n(n - 1)}{2} $
(4)$ \frac{35 × 34}{2} = 595 $
答案:595
(5)车站共有6个(深圳、惠州、陆丰、普宁、潮阳、潮汕),组合数为$ \frac{6 × 5}{2} = 15 $,往返车票种类为$ 15 × 2 = 30 $
答案:30
答案:15
(3)$ \frac{n(n - 1)}{2} $
答案:$ \frac{n(n - 1)}{2} $
(4)$ \frac{35 × 34}{2} = 595 $
答案:595
(5)车站共有6个(深圳、惠州、陆丰、普宁、潮阳、潮汕),组合数为$ \frac{6 × 5}{2} = 15 $,往返车票种类为$ 15 × 2 = 30 $
答案:30
查看更多完整答案,请扫码查看


