《2025年学习指要九年级数学上册人教版》

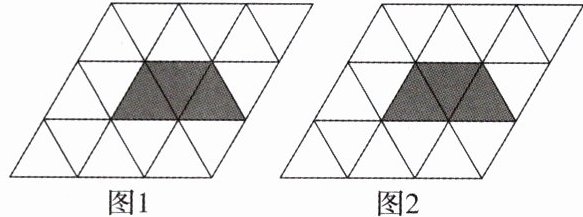
5. (2023 宁波期中)如图 1,图 2 都是由边长为 1 的小等边三角形构成的网格,每个网格图中有 3 个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,分别按下列要求选取 3 个涂上阴影：(请将两小题依次作答在图 1,图 2 中,均只需画出符合条件的一种情形)
(1)使得 6 个阴影小等边三角形组成一个轴对称图形而非中心对称图形；
(2)使得 6 个阴影小等边三角形组成一个中心对称图形而非轴对称图形。

答案：
(1) 如图 1，在余下空白小等边三角形中选取如图所示的 3 个涂上阴影，此时 6 个阴影小等边三角形组成一个轴对称图形而非中心对称图形。
(答案图1中除原阴影外新涂阴影位置合理，构成轴对称非中心对称即可)
(2) 如图 2，在余下空白小等边三角形中选取如图所示的 3 个涂上阴影，此时 6 个阴影小等边三角形组成一个中心对称图形而非轴对称图形。
(答案图2中除原阴影外新涂阴影位置合理，构成中心对称非轴对称即可)

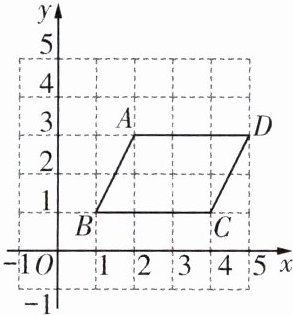
6. (2024 台州期末)如图,在平面直角坐标系中,四边形 $ABCD$ 的顶点坐标分别为 $A(2,3)$,$B(1,1)$,$C(4,1)$,$D(5,3)$。
(1)四边形 $ABCD$ 是中心对称图形吗？若是,请画出对称中心点 $E$；
(2)若点 $F(a,3)$ 在 $AD$ 上,在 $BC$ 上确定一点 $G$,使得 $FG$ 平分四边形 $ABCD$ 的面积,则 $G$ 点的坐标为____(6-a,1)。

(1) 是中心对称图形。对称中心点E(3,2)。

答案：
(1) 是中心对称图形。
连接AC、BD，交点E为对称中心。
A(2,3)，C(4,1)，AC中点坐标为$(\frac{2+4}{2},\frac{3+1}{2})=(3,2)$；
B(1,1)，D(5,3)，BD中点坐标为$(\frac{1+5}{2},\frac{1+3}{2})=(3,2)$。
故对称中心E(3,2)。
(2) 四边形ABCD为平行四边形，对称中心E(3,2)。FG平分面积，则FG必过E。
设G(b,1)，F(a,3)，E(3,2)三点共线。
由中点坐标公式：$\frac{a+b}{2}=3$，$\frac{3+1}{2}=2$（纵坐标恒成立）。
解得$b=6-a$。
故G点坐标为$(6-a,1)$。
(1) 对称中心点E(3,2)；
(2)$(6-a,1)$

思考 如何在平面直角坐标系中作关于原点对称的图形？

答案： 见解析

练习 已知点 $ M $ 的坐标为 $ (3,-5) $,则关于 $ x $ 轴对称的点的坐标为$(3,5)$,关于 $ y $ 轴对称的点的坐标为$(-3,-5)$,关于原点对称的点的坐标为$(-3,5)$。

答案： 关于$x$轴对称的点的坐标为$(3,5)$，关于$y$轴对称的点的坐标为$(-3,-5)$，关于原点对称的点的坐标为$(-3,5)$。
故答案依次为：$(3,5)$；$(-3,-5)$；$(-3,5)$。

探究一 求关于原点对称的点的坐标
例 1 (1)(2024 扬州中考)在平面直角坐标系中,点 $ P(1,2) $ 关于原点的对称点 $ P' $ 的坐标是(D)
A. $ (1,2) $
B. $ (-1,2) $
C. $ (1,-2) $
D. $ (-1,-2) $
(2)(2024 凉山中考)点 $ P(a,-3) $ 关于原点对称的点是 $ P'(2,b) $,则 $ a + b = $(A)
A. 1
B. -1
C. -5
D. 5
名师导引 在平面直角坐标系中,两个点关于原点对称时,这两个点的横坐标互为相反数,纵坐标也互为相反数；两个点关于 $ x $ 轴对称时,横坐标相同,纵坐标互为相反数；两个点关于 $ y $ 轴对称时,横坐标互为相反数,纵坐标相同。

答案：
(1) D
(2) A