第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
例1 (2023通辽中考改编)如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD= 24°,则旋转角α的度数为

名师导引 利用旋转的性质解决问题时,要抓住旋转角、对应线段、对应角相等的性质,尤其要注意当旋转角或者对应角为60°时容易形成等边三角形。
48
°。
名师导引 利用旋转的性质解决问题时,要抓住旋转角、对应线段、对应角相等的性质,尤其要注意当旋转角或者对应角为60°时容易形成等边三角形。
答案:
由题意知,将△ABC绕点A逆时针旋转到△ADE,
根据旋转的性质,有$AB = AD$,$\angle BAC = \angle DAE$,
因为$\angle BAC = \angle BAD + \angle CAD$,$\angle DAE = \angle DAE(自身)$,
所以,$\angle BAD = \angle DAE - \angle CAD = \alpha - 24°$(其中$\alpha$为旋转角),
由于$AB = AD$,根据等腰三角形的性质,有$\angle B = \angle ADB$,
在$\triangle ABD$中,根据三角形内角和为$180°$,
有$\angle B + \angle ADB + \angle BAD = 180°$,
代入$\angle B = \angle ADB$和$\angle BAD = \alpha - 24°$,
得$2\angle B + \alpha - 24° = 180°$,
即$\angle B = 102° - \frac{\alpha}{2}$,
因为$DE \perp AC$,
所以,$\angle E = 90° - \angle CAD = 66°$,
由于$\angle ADE = \angle B$(旋转性质),
所以,$\angle ADE = 102° - \frac{\alpha}{2}$,
在$\triangle ADE$中,根据三角形内角和为$180°$,
有$\angle ADE + \angle E + \angle DAE = 180°$,
代入$\angle ADE = 102° - \frac{\alpha}{2}$,$\angle E = 66°$,$\angle DAE = \alpha$,
得$102° - \frac{\alpha}{2} + 66° + \alpha = 180°$,
解得$\alpha = 24 × 2 = 48°$。
故答案为$48$。
根据旋转的性质,有$AB = AD$,$\angle BAC = \angle DAE$,
因为$\angle BAC = \angle BAD + \angle CAD$,$\angle DAE = \angle DAE(自身)$,
所以,$\angle BAD = \angle DAE - \angle CAD = \alpha - 24°$(其中$\alpha$为旋转角),
由于$AB = AD$,根据等腰三角形的性质,有$\angle B = \angle ADB$,
在$\triangle ABD$中,根据三角形内角和为$180°$,
有$\angle B + \angle ADB + \angle BAD = 180°$,
代入$\angle B = \angle ADB$和$\angle BAD = \alpha - 24°$,
得$2\angle B + \alpha - 24° = 180°$,
即$\angle B = 102° - \frac{\alpha}{2}$,
因为$DE \perp AC$,
所以,$\angle E = 90° - \angle CAD = 66°$,
由于$\angle ADE = \angle B$(旋转性质),
所以,$\angle ADE = 102° - \frac{\alpha}{2}$,
在$\triangle ADE$中,根据三角形内角和为$180°$,
有$\angle ADE + \angle E + \angle DAE = 180°$,
代入$\angle ADE = 102° - \frac{\alpha}{2}$,$\angle E = 66°$,$\angle DAE = \alpha$,
得$102° - \frac{\alpha}{2} + 66° + \alpha = 180°$,
解得$\alpha = 24 × 2 = 48°$。
故答案为$48$。
巩固提升 (2024无锡中考)如图,在△ABC中,∠B= 80°,∠C= 65°,将△ABC绕点A逆时针旋转得到△AB'C'。当AB'落在AC时,∠BAC'= (

A.65°
B.70°
C.80°
D.85°
B
)
A.65°
B.70°
C.80°
D.85°
答案:
B
例2 (1)(2023大庆中考)下列图标中,其文字上方的图案是中心对称图形的是(

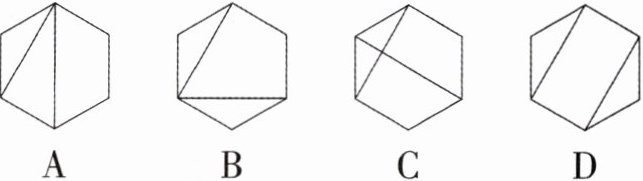
(2)(2023泰安中考)小亮以四种不同的方式连接正六边形的两条对角线,得到如下四种图形,则既是轴对称图形,又是中心对称图形的是(
名师导引 识别中心对称图形可以从以下两方面着手:(1)基本图形的个数是偶数;(2)相对的两个基本图形的对称点在一条过对称中心点的直线上,且对称点到对称中心的距离相等。
C
)
(2)(2023泰安中考)小亮以四种不同的方式连接正六边形的两条对角线,得到如下四种图形,则既是轴对称图形,又是中心对称图形的是(
C
)
名师导引 识别中心对称图形可以从以下两方面着手:(1)基本图形的个数是偶数;(2)相对的两个基本图形的对称点在一条过对称中心点的直线上,且对称点到对称中心的距离相等。
答案:
(1)C;
(2)C
(1)C;
(2)C
巩固提升 (2023齐齐哈尔中考)下列图形中,既是轴对称图形,又是中心对称图形的是(

A.
B.
C.
D.
D
)
A.
B.
C.
D.
答案:
D
例3 (2024丰都期末)点M(a - 1,-3)关于原点对称的点是N(2,b + 1),则a + b的值是
名师导引 若两个点关于原点对称,则它们的坐标符号相反。
1
。名师导引 若两个点关于原点对称,则它们的坐标符号相反。
答案:
1(这里按题目要求应填数值,若为填空题形式此为答案)
巩固提升 (2024海南期中)点P(-3,-1)关于x轴对称的点的坐标是
(-3,1)
,关于y轴对称的点的坐标是(3,-1)
,关于原点对称的点的坐标是(3,1)
。
答案:
$(-3,1)$,$(3,-1)$,$(3,1)$
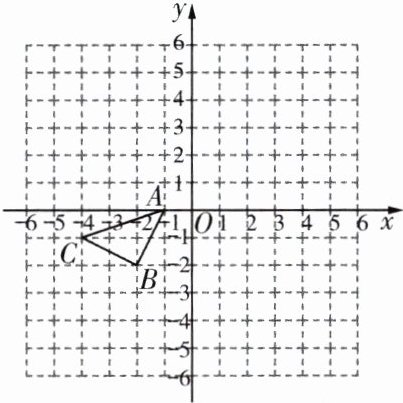
例4 (2024无锡期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(-2,-2),C(-3,-1)。按要求画图和答题:
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到图形$△AB_1C_1,$画出$△AB_1C_1。$
(2)画出△ABC关于坐标原点O成中心对称的$△A_2B_2C_2。$
(3)若$△A_2B_2C_2$可看作是由$△AB_1C_1$旋转得来,则旋转中心坐标为______。
(1) 画图略(△AB₁C₁顶点坐标:A(-1,0),B₁(-3,1),C₁(-2,2))。
(2) 画图略(△A₂B₂C₂顶点坐标:A₂(1,0),B₂(2,2),C₂(3,1))。
(3)(0,-1)
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到图形$△AB_1C_1,$画出$△AB_1C_1。$
(2)画出△ABC关于坐标原点O成中心对称的$△A_2B_2C_2。$
(3)若$△A_2B_2C_2$可看作是由$△AB_1C_1$旋转得来,则旋转中心坐标为______。

(1) 画图略(△AB₁C₁顶点坐标:A(-1,0),B₁(-3,1),C₁(-2,2))。
(2) 画图略(△A₂B₂C₂顶点坐标:A₂(1,0),B₂(2,2),C₂(3,1))。
(3)(0,-1)
答案:
(1) 画图略(△AB₁C₁顶点坐标:A(-1,0),B₁(-3,1),C₁(-2,2))。
(2) 画图略(△A₂B₂C₂顶点坐标:A₂(1,0),B₂(2,2),C₂(3,1))。
(3) (0,-1)
(1) 画图略(△AB₁C₁顶点坐标:A(-1,0),B₁(-3,1),C₁(-2,2))。
(2) 画图略(△A₂B₂C₂顶点坐标:A₂(1,0),B₂(2,2),C₂(3,1))。
(3) (0,-1)
查看更多完整答案,请扫码查看


