第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
2.(2023 宿迁中考)在同一平面内,已知 $\odot O$ 的半径为 $2$,圆心 $O$ 到直线 $l$ 的距离为 $3$,点 $P$ 为圆上的一个动点,则点 $P$ 到直线 $l$ 的最大距离是(
A.$2$
B.$5$
C.$6$
D.$8$
B
)A.$2$
B.$5$
C.$6$
D.$8$
答案:
B
3.(2024 天津期中)如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$,以 $C$ 为圆心、$CB$ 为半径的圆交 $AB$ 于点 $D$,连接 $CD$,则 $\angle ACD = ($
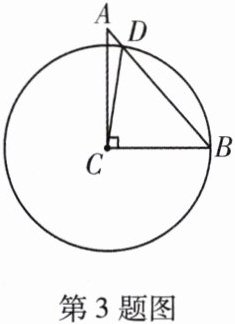
A.$15^{\circ}$
B.$10^{\circ}$
C.$12^{\circ}$
D.$50^{\circ}$
B
)
A.$15^{\circ}$
B.$10^{\circ}$
C.$12^{\circ}$
D.$50^{\circ}$
答案:
B
4.(2023 渝北区半期)如图,$MN$ 为 $\odot O$ 的弦,$\angle N = 50^{\circ}$,则 $\angle MON$ 的度数为
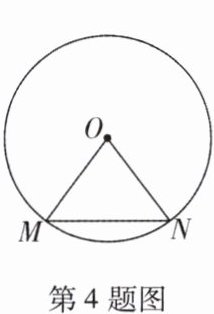
80
$^{\circ}$。
答案:
80
5.(2025 西双版纳一模)如图,$AB$ 是 $\odot O$ 的直径,$AC = CD$,$\angle AOC = 50^{\circ}$,则 $\angle BOD = $
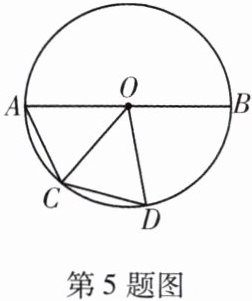
80
$^{\circ}$。
答案:
$80$
6.(2023 亳州期末)如图,直角 $\triangle ABC$ 的斜边 $AB$ 为 $\odot O$ 的一条弦,直角边 $AC$ 经过圆心 $O$,已知 $BC = 3$,$AC = 4$,则 $OA$ 的长为
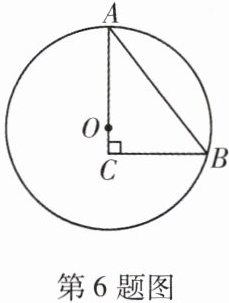
$\frac{25}{8}$
。
答案:
$\frac{25}{8}$
7. 如图,$\odot O$ 的弦 $AB$、半径 $OC$ 的延长线交于点 $D$,且 $BD = OA$。若 $\angle AOC = 120^{\circ}$,求 $\angle D$ 的度数。
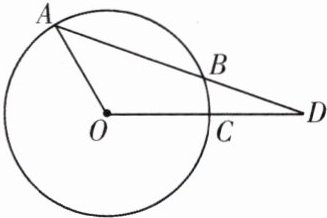

答案:
连接OB。
设∠D=x。
∵OA=OB=OC(同圆半径相等),BD=OA,
∴OB=BD,
∴∠BOD=∠BDO=x(等腰三角形底角相等)。
∵∠AOC=120°,D在OC延长线上,
∴∠AOD=120°。
在△AOD中,∠OAD=180°-∠AOD-∠D=180°-120°-x=60°-x。
∵OA=OB,
∴∠OBA=∠OAB=60°-x。
在△OBD中,∠OBD=180°-∠BOD-∠BDO=180°-2x。
∵点A、B、D共线,
∴∠OBA+∠OBD=180°,即(60°-x)+(180°-2x)=180°。
解得3x=60°,x=20°。
∠D=20°。
设∠D=x。
∵OA=OB=OC(同圆半径相等),BD=OA,
∴OB=BD,
∴∠BOD=∠BDO=x(等腰三角形底角相等)。
∵∠AOC=120°,D在OC延长线上,
∴∠AOD=120°。
在△AOD中,∠OAD=180°-∠AOD-∠D=180°-120°-x=60°-x。
∵OA=OB,
∴∠OBA=∠OAB=60°-x。
在△OBD中,∠OBD=180°-∠BOD-∠BDO=180°-2x。
∵点A、B、D共线,
∴∠OBA+∠OBD=180°,即(60°-x)+(180°-2x)=180°。
解得3x=60°,x=20°。
∠D=20°。
新知梳理
1. 圆是轴对称图形,任何一条
思考 如何证明圆是轴对称图形?
2. 垂径定理:垂直于弦的直径
思考 垂径定理的条件和结论分别是什么?
3. 推论:平分弦(不是直径)的直径
思考 若被直径平分的弦是直径,上面的推论还成立吗?
1. 圆是轴对称图形,任何一条
直径
所在直线都是圆的对称轴。思考 如何证明圆是轴对称图形?
2. 垂径定理:垂直于弦的直径
平分
弦,并且平分
弦所对的两条弧。思考 垂径定理的条件和结论分别是什么?
3. 推论:平分弦(不是直径)的直径
垂直于
弦,并且平分
弦所对的两条弧。思考 若被直径平分的弦是直径,上面的推论还成立吗?
答案:
1. 直径;
2. 平分,平分;
3. 垂直于,平分;
1. (思考题答案不要求)
2. (思考题答案不要求)
3. (思考题答案不要求)
2. 平分,平分;
3. 垂直于,平分;
1. (思考题答案不要求)
2. (思考题答案不要求)
3. (思考题答案不要求)
探究 垂径定理的运用
例(2023 永州中考改编)
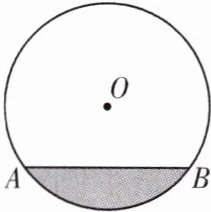
如图,$\odot O$是一个盛有水的容器的横截面,$\odot O$的半径为 10 cm. 水的最深处到水面$AB$的距离为 4 cm,求水面$AB$的宽度。
名师导引 解决有关弦的问题时,常常需要作辅助线“垂直于弦的直径”,以圆的半径、弦长的一半、圆心到弦的垂线段为三边构造直角三角形。
例(2023 永州中考改编)

如图,$\odot O$是一个盛有水的容器的横截面,$\odot O$的半径为 10 cm. 水的最深处到水面$AB$的距离为 4 cm,求水面$AB$的宽度。
名师导引 解决有关弦的问题时,常常需要作辅助线“垂直于弦的直径”,以圆的半径、弦长的一半、圆心到弦的垂线段为三边构造直角三角形。
答案:
解:过点O作OC⊥AB于点C,延长OC交⊙O于点D,连接OA。
∵OC⊥AB,
∴AC=BC=$\frac{1}{2}$AB。
∵⊙O的半径为10cm,
∴OA=OD=10cm。
∵水的最深处到水面AB的距离为4cm,
∴CD=4cm,
∴OC=OD-CD=10-4=6cm。
在Rt△OAC中,OA=10cm,OC=6cm,
由勾股定理得:AC=$\sqrt{OA^{2}-OC^{2}}=\sqrt{10^{2}-6^{2}}=\sqrt{100-36}=\sqrt{64}=8$cm。
∴AB=2AC=2×8=16cm。
答:水面AB的宽度为16cm。
∵OC⊥AB,
∴AC=BC=$\frac{1}{2}$AB。
∵⊙O的半径为10cm,
∴OA=OD=10cm。
∵水的最深处到水面AB的距离为4cm,
∴CD=4cm,
∴OC=OD-CD=10-4=6cm。
在Rt△OAC中,OA=10cm,OC=6cm,
由勾股定理得:AC=$\sqrt{OA^{2}-OC^{2}}=\sqrt{10^{2}-6^{2}}=\sqrt{100-36}=\sqrt{64}=8$cm。
∴AB=2AC=2×8=16cm。
答:水面AB的宽度为16cm。
查看更多完整答案,请扫码查看


