《2025年基础训练大象出版社七年级数学上册人教版》

7. 某学校食堂有$m$t煤,计划每天用$n$t煤,实际每天节约$a$t煤,节约后可多用的天数为【B】
A.$\frac {m}{n+a}-\frac {m}{n}$
B.$\frac {m}{n-a}-\frac {m}{n}$
C.$\frac {m}{n}-\frac {m}{n+a}$
D.$\frac {m}{n}-\frac {m}{n-a}$

答案： B

8. 下列计算正确的是【B】
A.$3(a+b)= 3a+b$
B.$-a^{2}b+ba^{2}= 0$
C.$a^{2}+2a^{2}= 3a^{4}$
D.$3a^{2}-2a^{2}= 1$

答案： B

9. 若关于$x的多项式11x^{5}+16x^{2}-1与3x^{3}+4mx^{2}-15x+13$的和不含二次项,则$m$等于【D】
A.2
B.-2
C.4
D.-4

答案： D

10. 若$a,b$互为相反数,$c,d$互为倒数,则$2026a+2026b-\frac {21}{cd}$的值为【C】
A.2025
B.4026
C.-21
D.21

答案： C

11. 举一个生活情境的例子,说明$5x$的含义:例如，一个苹果$x$元，买$5$个苹果需要$5x$元（答案不唯一）。.

答案： 例如，一个苹果$x$元，买$5$个苹果需要$5x$元（答案不唯一）。

12. 多项式$-\frac {2\pi x^{2}y}{5}+2x-1$的次数是3.

答案： 3

13. 若$a_{1}= 1-\frac {3}{4},a_{2}= 1-\frac {1}{a_{1}},a_{3}= 1-\frac {1}{a_{2}},…$,则$a_{80}= $$-3$.

答案： $-3$（或写为$a_2$的值）

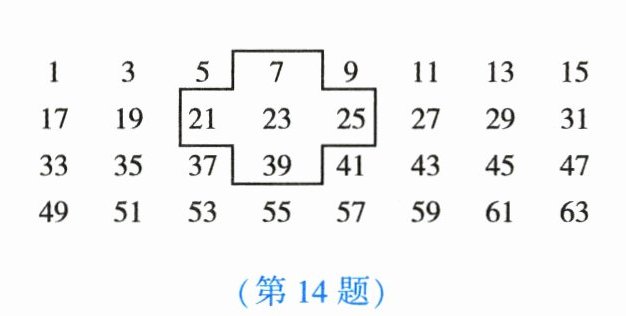
14. 将连续的奇数$1,3,5,7,9,…$排列成如图所示的数表.任意圈出如图所示的5个数,设中间的一个数为$a$,则这5个数之和是5a(用含$a$的代数式表示).

答案： 5a

15. 如图,已知正五角星的面积为5,正方形的边长为2,图中对应阴影部分的面积分别是$S_{1},S_{2}$,则$S_{1}-S_{2}$的值为1.

答案： 1