《2025年基础训练大象出版社七年级数学上册人教版》

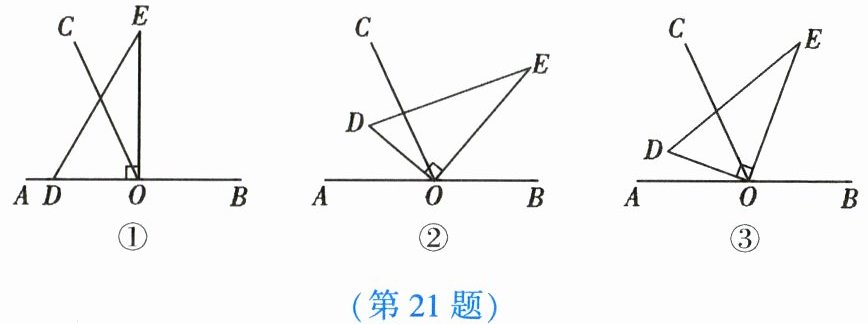
21. (10分)如图,以直线$AB上一点O为端点作射线OC$,使$\angle AOC = 65^{\circ}$,将一个直角三角板的直角顶点放在点$O$处.(注:$\angle DOE = 90^{\circ}$)
(1) 如图①,若直角三角板$DOE的一边OD放在射线OA$上,则$\angle COE$的度数为25°;
(2) 如图②,将直角三角板$DOE绕点O$顺时针转动到某个位置,若$OC恰好平分\angle AOE$,求$\angle COD$的度数;
(3) 如图③,将直角三角板$DOE绕点O$任意转动,如果$OD始终在\angle AOC$的内部,试猜想$\angle AOD和\angle COE$有怎样的数量关系,并说明理由.

答案：
(1)
∵OD在射线OA上，∠DOE=90°，
∴∠AOE=∠DOE=90°。
∵∠AOC=65°，
∴∠COE=∠AOE - ∠AOC=90° - 65°=25°。
故答案为25°。
(2)
∵OC平分∠AOE，∠AOC=65°，
∴∠COE=∠AOC=65°。
∵∠DOE=90°，
∴∠COD=∠DOE - ∠COE=90° - 65°=25°。
(3) ∠COE - ∠AOD=25°。
理由：设∠AOD=x，
∵OD在∠AOC内部，
∴∠DOC=∠AOC - ∠AOD=65° - x。
∵∠DOE=90°，
∴∠COE=∠DOE - ∠DOC=90° - (65° - x)=x + 25°。
∴∠COE - ∠AOD=25°。