第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
19. (9分)如图,已知$\angle 1 = 19^{\circ}$,$\angle AOE = 90^{\circ}$,$OB平分\angle AOC$,$OD平分\angle COE$.
(1) 求$\angle 2$的度数;
(2) 若以点$O$为观察中心,以$OE$为正北方向,则从方位角来说,射线$OD$在什么方向?
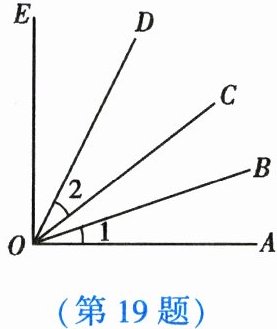
(1) 求$\angle 2$的度数;
(2) 若以点$O$为观察中心,以$OE$为正北方向,则从方位角来说,射线$OD$在什么方向?

答案:
(1)26°;
(2)北偏东26°方向.
(1)26°;
(2)北偏东26°方向.
20. (10分)如图,已知点$B,C在线段AD$上.
(1) 图中共有
(2) 图中$AB = CD$.
①比较线段的长短:$AC$
②若$BD = 4AB$,$BC = 12\ cm$,则线段$AD$的长为
(3) 若$CD = 2AB$,且$E为BC$的中点,求线段$AE与线段BD$间的数量关系.(温馨提醒:重新画图)

(1) 图中共有
6
条线段.(2) 图中$AB = CD$.
①比较线段的长短:$AC$
=
$BD$;(填“$>$”“$=$”或“$<$”)②若$BD = 4AB$,$BC = 12\ cm$,则线段$AD$的长为
20
$cm$.(3) 若$CD = 2AB$,且$E为BC$的中点,求线段$AE与线段BD$间的数量关系.(温馨提醒:重新画图)

设$AB = x$,则$CD = 2x$,设$BC = y$,$E$为$BC$中点,所以$BE = \frac{y}{2}$。$AE = AB + BE = x + \frac{y}{2}$,$BD = BC + CD = y + 2x$。则$BD = 2x + y = 2\left(x + \frac{y}{2}\right) = 2AE$,故$BD = 2AE$。
答案:
(1) 6
(2) ①=
②设$AB = CD = x$,则$BD = BC + CD = 12 + x$。
因为$BD = 4AB$,所以$12 + x = 4x$,解得$x = 4$。
$AD = AB + BC + CD = 4 + 12 + 4 = 20$,故答案为20。
(3) 设$AB = x$,则$CD = 2x$,设$BC = y$,$E$为$BC$中点,所以$BE = \frac{y}{2}$。
$AE = AB + BE = x + \frac{y}{2}$,$BD = BC + CD = y + 2x$。
则$BD = 2x + y = 2\left(x + \frac{y}{2}\right) = 2AE$,故$BD = 2AE$。
(1) 6
(2) ①=
②设$AB = CD = x$,则$BD = BC + CD = 12 + x$。
因为$BD = 4AB$,所以$12 + x = 4x$,解得$x = 4$。
$AD = AB + BC + CD = 4 + 12 + 4 = 20$,故答案为20。
(3) 设$AB = x$,则$CD = 2x$,设$BC = y$,$E$为$BC$中点,所以$BE = \frac{y}{2}$。
$AE = AB + BE = x + \frac{y}{2}$,$BD = BC + CD = y + 2x$。
则$BD = 2x + y = 2\left(x + \frac{y}{2}\right) = 2AE$,故$BD = 2AE$。
查看更多完整答案,请扫码查看


