第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
7. 按如图所示的程序计算,若开始输入的$x$值是正整数,最后输出的结果是32,则满足条件的$x$值为【
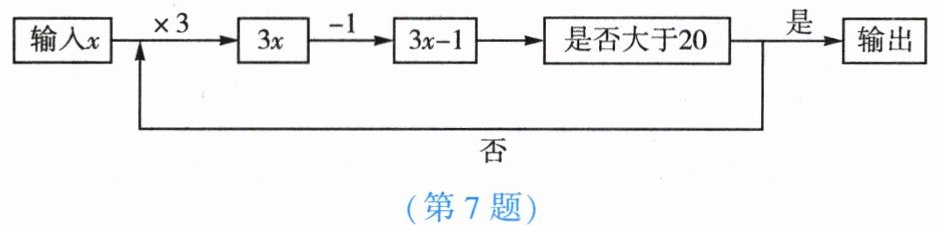
A.11
B.4
C.11或4
D.无法确定
C
】
A.11
B.4
C.11或4
D.无法确定
答案:
C
8. 将一个正方形剪成$n$个小正方形,第一次操作按照图①所示,分割出4个小正方形;第二次操作按照图②所示,分割出6个小正方形;第三次操作按照图③所示,分割出8个小正方形;……按照上述规律,则第$n$次操作,得到小正方形的个数为【

A.$(n + 1)^{2}$
B.$3n + 1$
C.$2n$
D.$2n + 2$
D
】
A.$(n + 1)^{2}$
B.$3n + 1$
C.$2n$
D.$2n + 2$
答案:
D
9. 某商店为了回馈客户,将原价为8元/本的笔记本进行优惠出售,方案如下:方案一,一次性购买不超过100本,按原价销售;方案二,一次性购买100本以上,每本便宜2元.若购买$n本笔记本需a$元,则下列说法正确的是【
A.当$n = 100$时,$a = 600$
B.当$a = 624$时,$n = 78$
C.存在买$n(n$小于100)本笔记本所需钱数比买200本笔记本所需钱数多
D.存在买$n(n$大于100)本笔记本所需钱数比买80本笔记本所需钱数少
D
】A.当$n = 100$时,$a = 600$
B.当$a = 624$时,$n = 78$
C.存在买$n(n$小于100)本笔记本所需钱数比买200本笔记本所需钱数多
D.存在买$n(n$大于100)本笔记本所需钱数比买80本笔记本所需钱数少
答案:
D
10. 观察下列一组数:$-2,\frac{4}{3},-\frac{8}{5},\frac{16}{7},-\frac{32}{9},…$.它们是按照一定规律排列的,那么这组数的第$n$个数是【
A.$\frac{-2^{n}}{2n + 1}$
B.$\frac{(-2)^{n}}{2n + 1}$
C.$\frac{(-2)^{n}}{2n - 1}$
D.$\frac{-2^{n}}{2n - 1}$
C
】A.$\frac{-2^{n}}{2n + 1}$
B.$\frac{(-2)^{n}}{2n + 1}$
C.$\frac{(-2)^{n}}{2n - 1}$
D.$\frac{-2^{n}}{2n - 1}$
答案:
C
11. $x$的一半与5的差,用代数式可表示为
$\frac{x}{2}-5$
.
答案:
$\frac{x}{2}-5$
12. 某市今年新安装了供暖管道.已知该市去年安装了$a$条,今年改革后,安装的管道数量比去年的2倍多6条,则今年安装供暖管道
$2a + 6$
条.
答案:
$2a + 6$
13. 小明说:“请你任意想一个数,把这个数乘$-3$后加12,然后除以6,再加上你原来所想的那个数的一半,我可以知道你计算的结果.”请你写出这个计算结果:
2
.
答案:
2
查看更多完整答案,请扫码查看


