第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
14. 一棵树的高度$h$m与栽种后的生长时间$n$年之间满足一定的关系,根据下表中的数据,可知$h= $
| $n/$年 | 0 | 1 | 2 | 3 | 4 | …$$ |
| $h/$m | 2.6 | 3.2 | 3.8 | 4.4 | 5.0 | …$$ |

$0.6n + 2.6$
(用含$n$的代数式表示).| $n/$年 | 0 | 1 | 2 | 3 | 4 | …$$ |
| $h/$m | 2.6 | 3.2 | 3.8 | 4.4 | 5.0 | …$$ |

答案:
$0.6n + 2.6$
15. 如图,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图中“●”的个数为3,第2幅图中“●”的个数为8,第3幅图中“●”的个数为15……以此类推,则第$n$幅图中“●”的个数为
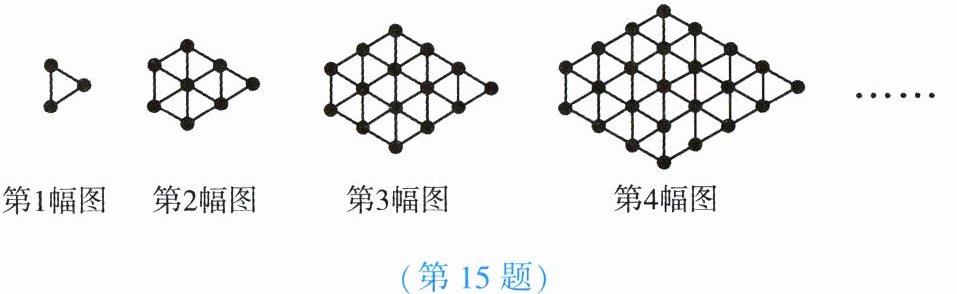
$n^{2}+2n$
.
答案:
$n^{2}+2n$
16. (8分)已知$a,b$互为相反数,$c,d$互为倒数,数轴上表示$m$的点到原点的距离为3,求$\frac{a + b}{m}+cd - m$的值.
答案:
因为$a$,$b$互为相反数,所以$a + b=0$;
因为$c$,$d$互为倒数,所以$cd = 1$;
因为数轴上表示$m$的点到原点的距离为$3$,所以$|m|=3$,即$m = 3$或$m=- 3$。
当$m = 3$时,$\frac{a + b}{m}+cd - m=\frac{0}{3}+1 - 3=0 + 1-3=-2$;
当$m=-3$时,$\frac{a + b}{m}+cd - m=\frac{0}{-3}+1-(-3)=0 + 1 + 3=4$。
综上,$\frac{a + b}{m}+cd - m$的值为$-2$或$4$。
因为$c$,$d$互为倒数,所以$cd = 1$;
因为数轴上表示$m$的点到原点的距离为$3$,所以$|m|=3$,即$m = 3$或$m=- 3$。
当$m = 3$时,$\frac{a + b}{m}+cd - m=\frac{0}{3}+1 - 3=0 + 1-3=-2$;
当$m=-3$时,$\frac{a + b}{m}+cd - m=\frac{0}{-3}+1-(-3)=0 + 1 + 3=4$。
综上,$\frac{a + b}{m}+cd - m$的值为$-2$或$4$。
17. (9分)某校为了迎接世界读书日,开展了“沐浴书香,润泽人生”课本剧表演活动,并设立了一、二、三等奖,根据需要购买了50件奖品,其中二等奖奖品的数量比一等奖奖品的数量的3倍少2件,各种奖品的单价和数量如下表所示:
| | 一等奖奖品 | 二等奖奖品 | 三等奖奖品 |
| 单价/(元/件) | 20 | 14 | 8 |
| 数量/件 | $x$ | ______ | ______ |

(1) 用含$x$的式子表示:二等奖奖品的数量是
(2) 求购买这50件奖品所需的总费用.(用含$x$的式子表示,结果化为最简形式)
| | 一等奖奖品 | 二等奖奖品 | 三等奖奖品 |
| 单价/(元/件) | 20 | 14 | 8 |
| 数量/件 | $x$ | ______ | ______ |

(1) 用含$x$的式子表示:二等奖奖品的数量是
$3x - 2$
件,三等奖奖品的数量是______$52 - 4x$
件;(2) 求购买这50件奖品所需的总费用.(用含$x$的式子表示,结果化为最简形式)
答案:
(1)
二等奖奖品的数量是$(3x - 2)$件;
三等奖奖品的数量是$50 - x - (3x - 2)=52 - 4x$件。
(2)
总费用$W = 20x + 14(3x - 2) + 8(52 - 4x)$
$=20x + 42x - 28 + 416 - 32x$
$=(20x + 42x - 32x)+(416 - 28)$
$= 30x + 388$。
故购买这$50$件奖品所需的总费用为$(30x + 388)$元。
二等奖奖品的数量是$(3x - 2)$件;
三等奖奖品的数量是$50 - x - (3x - 2)=52 - 4x$件。
(2)
总费用$W = 20x + 14(3x - 2) + 8(52 - 4x)$
$=20x + 42x - 28 + 416 - 32x$
$=(20x + 42x - 32x)+(416 - 28)$
$= 30x + 388$。
故购买这$50$件奖品所需的总费用为$(30x + 388)$元。
查看更多完整答案,请扫码查看


