第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
2. 解不等式:$(2x + 3)(2x - 3) < 4(x - 1) \cdot (x + 4)$.
答案:
2.$x>\frac {7}{12}.$
例 3 如图,大正方形与小正方形的面积之差是 36,则图中阴影部分的面积是______.
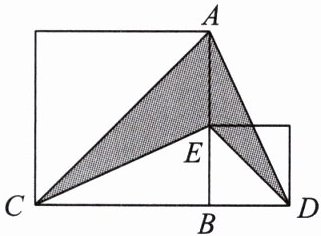

答案:
18
3. 【探究】
如图①,从边长为$a的大正方形中剪掉一个边长为b$的小正方形,将阴影部分沿虚线剪开,拼成图②所示的长方形.
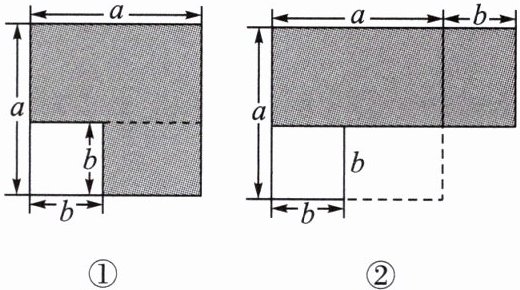
(1)请你分别表示出这两个图形中阴影部分的面积:______,______.
(2)比较图①、图②中阴影部分的面积,可以得到乘法公式:______.(用字母表示)
【应用】
请应用上述公式计算:$(2a + b - c)(2a - b + c)$.
【拓展】
(1)计算$(2 + 1)(2^{2} + 1)(2^{4} + 1)(2^{8} + 1) …\cdot \cdot (2^{32} + 1) + 1$的结果的个位数字为______;
(2)计算:$200^{2} - 199^{2} + 198^{2} - 197^{2} + … + 4^{2} - 3^{2} + 2^{2} - 1^{2}$.
如图①,从边长为$a的大正方形中剪掉一个边长为b$的小正方形,将阴影部分沿虚线剪开,拼成图②所示的长方形.

(1)请你分别表示出这两个图形中阴影部分的面积:______,______.
(2)比较图①、图②中阴影部分的面积,可以得到乘法公式:______.(用字母表示)
【应用】
请应用上述公式计算:$(2a + b - c)(2a - b + c)$.
【拓展】
(1)计算$(2 + 1)(2^{2} + 1)(2^{4} + 1)(2^{8} + 1) …\cdot \cdot (2^{32} + 1) + 1$的结果的个位数字为______;
(2)计算:$200^{2} - 199^{2} + 198^{2} - 197^{2} + … + 4^{2} - 3^{2} + 2^{2} - 1^{2}$.
答案:
3.【探究】
(1)$a^{2}-b^{2}$ $(a+b)(a-b)$
(2)$a^{2}-b^{2}=(a+b)(a-b)$【应用】$4a^{2}-b^{2}+2bc-c^{2}.$【拓展】
(1)6
(2)20 100.
(1)$a^{2}-b^{2}$ $(a+b)(a-b)$
(2)$a^{2}-b^{2}=(a+b)(a-b)$【应用】$4a^{2}-b^{2}+2bc-c^{2}.$【拓展】
(1)6
(2)20 100.
查看更多完整答案,请扫码查看


