第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
1 如图,数轴上点 $ M $,$ E $,$ F $,$ N $ 表示的数分别是 $-4$,$-3$,$-1$,$3$.
(1) 点 $ M $ 与点 $ N $ 之间的距离是
(2) 点 $ E $ 与点 $ F $ 之间的距离是
(3) 若数轴上的两个点之间的距离为 $ 5 $,其中一个点表示的数为 $-3$,则另一个点表示的数是
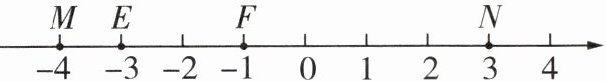
(1) 点 $ M $ 与点 $ N $ 之间的距离是
7
;(2) 点 $ E $ 与点 $ F $ 之间的距离是
2
;(3) 若数轴上的两个点之间的距离为 $ 5 $,其中一个点表示的数为 $-3$,则另一个点表示的数是
2或-8
.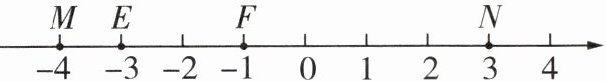
答案:
1
(1)7;
(2)2;
(3)2或-8
(3)当另一个点在-3所表示的点的右侧时,另一个点表示的数为2;当另一个点在-3所表示的点的左侧时,另一个点表示的数为-8.
(1)7;
(2)2;
(3)2或-8
(3)当另一个点在-3所表示的点的右侧时,另一个点表示的数为2;当另一个点在-3所表示的点的左侧时,另一个点表示的数为-8.
2 有两只蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点 $ A $ 的位置沿数轴向右爬了 $ 4 $ 个单位长度到达点 $ C $ 处,蚂蚁乙从图中点 $ B $ 的位置沿数轴向左爬了 $ 8 $ 个单位长度到达点 $ D $ 处.
(1) 在图中描出点 $ C $,$ D $ 的位置;
(2) 点 $ E $ 到点 $ C $ 与点 $ D $ 的距离相等,在数轴上描出点 $ E $ 的位置,并用“$<$”号把点 $ A $,$ B $,$ C $,$ D $,$ E $ 所表示的数连接起来.
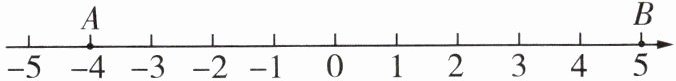
(1) 在图中描出点 $ C $,$ D $ 的位置;
(2) 点 $ E $ 到点 $ C $ 与点 $ D $ 的距离相等,在数轴上描出点 $ E $ 的位置,并用“$<$”号把点 $ A $,$ B $,$ C $,$ D $,$ E $ 所表示的数连接起来.
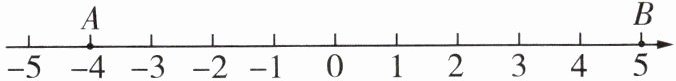
答案:
2 解:
(1)由题意,得点C表示的数为0,点D表示的数为-3,在数轴上描出点C,D的位置如图1所示.
(2)因为点E到点C与点D的距离相等,所以点E表示的数为-1.5.在数轴上描出点E的位置如图2所示. 把点A,B,C,D,E所表示的数用“<”号连接起来,得-4<-3<-1.5<0<5.
把点A,B,C,D,E所表示的数用“<”号连接起来,得-4<-3<-1.5<0<5.
2 解:
(1)由题意,得点C表示的数为0,点D表示的数为-3,在数轴上描出点C,D的位置如图1所示.

(2)因为点E到点C与点D的距离相等,所以点E表示的数为-1.5.在数轴上描出点E的位置如图2所示.
 把点A,B,C,D,E所表示的数用“<”号连接起来,得-4<-3<-1.5<0<5.
把点A,B,C,D,E所表示的数用“<”号连接起来,得-4<-3<-1.5<0<5. 3 [2025 北京怀柔区期末] 有理数 $ a $,$ b $,$ c $ 在数轴上的对应点的位置如图所示.若 $ b $ 与 $ c $ 互为相反数,则 $ a $,$ b $,$ c $ 中绝对值最大的数是 ( )

A.$ a $
B.$ b $
C.$ c $
D.无法确定

A.$ a $
B.$ b $
C.$ c $
D.无法确定
答案:
3 A 如图,因为b与c互为相反数,所以原点在b,c的中间,所以a距离原点最远,所以a,b,c中绝对值最大的数是a.
3 A 如图,因为b与c互为相反数,所以原点在b,c的中间,所以a距离原点最远,所以a,b,c中绝对值最大的数是a.

4 一题多解 若 $ a > 0 $,$ b < 0 $,$ a < |b| $,则 $ a $,$ b $,$-a$,$-b$ 的大小关系是 (
A.$ a > -b > -a > b $
B.$ a > -a > -b > b $
C.$ -b > a > -a > b $
D.$ a > b > -b > -a $
C
)A.$ a > -b > -a > b $
B.$ a > -a > -b > b $
C.$ -b > a > -a > b $
D.$ a > b > -b > -a $
答案:
4 C 通解 根据已知条件,可知表示a,b的点分别位于原点右侧和左侧,同时表示b的点距离原点较远,根据相反数的几何意义可得-a,-b在数轴上的位置(如图),根据数轴可知-b>a>-a>b. b−aoa−b 秒解(赋值法) 根据已知条件给a,b赋值,令a=2,b=-3,则-a=-2,-b=3,所以-b>a>-a>b.
5 新趋势·结论开放 有理数 $ b $ 在数轴上的对应点的位置如图中黑点所示.若整数 $ a $ 满足 $ |a| < |b| $,则整数 $ a $ 的值可以是

1(答案不唯一)
.
答案:
5 1(答案不唯一)
6 如图,一条流水线上依次有 $ 5 $ 个机器人,它们站的位置在数轴上依次用点 $ A_1 $,$ A_2 $,$ A_3 $,$ A_4 $,$ A_5 $ 表示.
(1) 点
(2) 若原点是零件供应点,则 $ 5 $ 个机器人到供应点取货的总路程是多少?
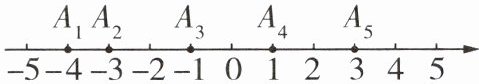
(1) 点
$A_2$
和点$A_5$
,点$A_3$
和点$A_4$
表示的数到原点的距离相等.(2) 若原点是零件供应点,则 $ 5 $ 个机器人到供应点取货的总路程是多少?
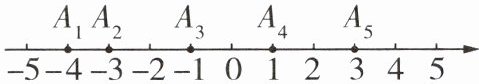
6 解:
(1)A₂ A₅ A₃ A₄ 因为|-3|=|3|,|-1|=|1|,所以点A₂和点A₅,点A₃和点A₄表示的数到原点的距离相等.
(2)由题意,得|-4|+|-3|+|-1|+|1|+|3|=12,所以5个机器人到供应点取货的总路程是12.
(1)A₂ A₅ A₃ A₄ 因为|-3|=|3|,|-1|=|1|,所以点A₂和点A₅,点A₃和点A₄表示的数到原点的距离相等.
(2)由题意,得|-4|+|-3|+|-1|+|1|+|3|=12,所以5个机器人到供应点取货的总路程是12.
答案:
6 解:
(1)A₂ A₅ A₃ A₄ 因为|-3|=|3|,|-1|=|1|,所以点A₂和点A₅,点A₃和点A₄表示的数到原点的距离相等.
(2)由题意,得|-4|+|-3|+|-1|+|1|+|3|=12,所以5个机器人到供应点取货的总路程是12.
(1)A₂ A₅ A₃ A₄ 因为|-3|=|3|,|-1|=|1|,所以点A₂和点A₅,点A₃和点A₄表示的数到原点的距离相等.
(2)由题意,得|-4|+|-3|+|-1|+|1|+|3|=12,所以5个机器人到供应点取货的总路程是12.
7 [2025 郑州三十七中月考] 如图,圆的周长为 $ 4 $ 个单位长度,圆周的 $ 4 $ 等分点分别为 $ A $,$ B $,$ C $,$ D $,先将圆上的点 $ A $ 与数轴上数 $ 1 $ 所对应的点重合,再将圆沿着数轴向左无滑动滚动,那么圆上与数轴上数 $-2025$ 所对应的点重合的点是 (

A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
C
)
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
答案:
7 C 因为数轴上表示1的点与表示-2025的点之间的距离是2026,2026÷4=506……2(每经过4个单位长度,圆滚动1圈;当圆滚动506圈时,点A在数轴上,此时需要再向左滚动2个单位长度,即可到达-2025所在的点),所以与-2025所对应的点重合的点是C.
8 在数轴上,点 $ A $ 从原点出发,第 $ 1 $ 次向右移动 $ 1 $ 个单位长度,第 $ 2 $ 次向左移动 $ 2 $ 个单位长度,第 $ 3 $ 次向右移动 $ 3 $ 个单位长度,第 $ 4 $ 次向左移动 $ 4 $ 个单位长度……则第 $ 2026 $ 次移动后,点 $ A $ 表示的数为
-1013
.
答案:
8 -1013 根据题意,可得点A第1次向右移动1个单位长度后,所在位置的点表示的数为1,第2次向左移动2个单位长度后,所在位置的点表示的数为-1,第3次向右移动3个单位长度后,所在位置的点表示的数为2,第4次向左移动4个单位长度后,所在位置的点表示的数为-2……(当n为偶数时,第n次移动后,点A表示的数为-$\frac{n}{2}$),则第2026次移动后,点A表示的数为-1013.
查看更多完整答案,请扫码查看


