第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
11 给出下列说法:①互为补角的两个角的平分线互相垂直;②在同一平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交;③两条直线相交形成四个角,若有一对对顶角互余,则这两条直线互相垂直;④画一条射线的垂线,垂足一定落在这条射线上。其中错误的是(
A.①②③
B.①③④
C.②③④
D.①②③④
①③④
)A.①②③
B.①③④
C.②③④
D.①②③④
答案:
B 互为邻补角的两个角的平分线互相垂直,①错误.两条直线相交形成四个角,若有一对对顶角互补,则这两条直线互相垂直,③错误.画一条射线的垂线,就是画它所在直线的垂线,垂足可能落在射线上,也可能落在射线的反向延长线上,④错误.
12 教材 P176 练习 T2 变式 根据下列要求作图。
(1)如图 1,过点$P作AB$的垂线;
(2)如图 2,过点$P分别作OA$,$OB$的垂线;
(3)如图 3,过点$A作BC$的垂线,并量出点$A到BC$的距离。
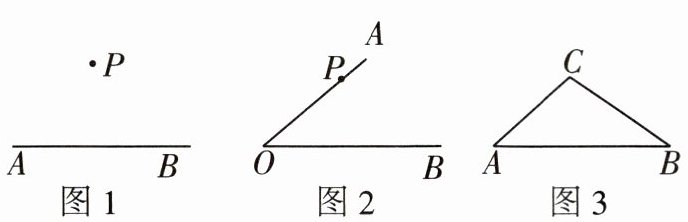
(1)如图 1,过点$P作AB$的垂线;
(2)如图 2,过点$P分别作OA$,$OB$的垂线;
(3)如图 3,过点$A作BC$的垂线,并量出点$A到BC$的距离。

答案:
解:
(1)如图1,直线PD即为所求.
(2)如图2,直线PE,PF即为所求.
(3)如图3,直线AH即为所求,点A到BC的距离大约是1cm.



解:
(1)如图1,直线PD即为所求.
(2)如图2,直线PE,PF即为所求.
(3)如图3,直线AH即为所求,点A到BC的距离大约是1cm.



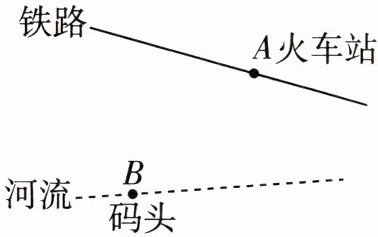
13 教材 P198 复习题 T4 变式 如图,两条直线分别表示铁路和河流,点$A$表示火车站,点$B$表示码头。
(1)从火车站$A到码头B$怎样走最近?画图并写出依据。
(2)从码头$B$到铁路怎样走最近?画图并写出依据。
(3)从火车站$A$到河流怎样走最近?画图并写出依据。
(1)从火车站$A到码头B$怎样走最近?画图并写出依据。
(2)从码头$B$到铁路怎样走最近?画图并写出依据。
(3)从火车站$A$到河流怎样走最近?画图并写出依据。

答案:
解:
(1)如图,从火车站A到码头B沿线段AB走最近,依据是两点之间线段最短.
(2)如图,从码头B到铁路沿垂线段BC走最近,依据是垂线段最短.
(3)如图,从火车站A到河流沿线段AD走最近,依据是垂线段最短.

解:
(1)如图,从火车站A到码头B沿线段AB走最近,依据是两点之间线段最短.
(2)如图,从码头B到铁路沿垂线段BC走最近,依据是垂线段最短.
(3)如图,从火车站A到河流沿线段AD走最近,依据是垂线段最短.

14 在学习相交线和平行线这一章时,李磊学习了垂直的定义,并仿照垂直的定义给出下面的新定义:若两条直线相交所形成的四个角中,有一个角是$60^{\circ}$,就称这两条直线互为完美交线,交点为完美点。已知直线$AB$,$CD$互为完美交线,$O$为它们的完美点,$OE\perp AB于点O$,求$\angle EOC$的度数。
答案:
解:①如图1,因为直线AB,CD互为完美交线,所以∠BOC=60°.因为OE⊥AB,所以∠BOE=90°,所以∠EOC=90° - 60°=30°.

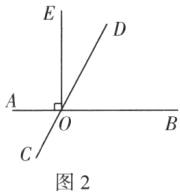
②如图2,因为直线AB,CD互为完美交线,所以∠AOC=60°.因为OE⊥AB,所以∠AOE=90°,所以∠EOC=90° + 60°=150°.综上,∠EOC的度数为30°或150°.
解:①如图1,因为直线AB,CD互为完美交线,所以∠BOC=60°.因为OE⊥AB,所以∠BOE=90°,所以∠EOC=90° - 60°=30°.


②如图2,因为直线AB,CD互为完美交线,所以∠AOC=60°.因为OE⊥AB,所以∠AOE=90°,所以∠EOC=90° + 60°=150°.综上,∠EOC的度数为30°或150°.
15 推理能力【问题情境】
如图,直线$AB$,$CD相交于点O$,$ON把\angle AOD$分成两个角,且$\angle AON:\angle NOD= 2:3$。
【问题提出】
(1)若$\angle BOC= 75^{\circ}$,求$\angle AON$的度数。
(2)在(1)的基础上,若$OM平分\angle BON$,则$OB是\angle COM$的平分线吗?并说明理由。
【问题解决】
(3)若$OM\perp ON于点O$,则$\frac{3}{5}\angle AOC-\angle DOM$是否为固定度数?若是,请求出该度数;若不是,请说明理由。
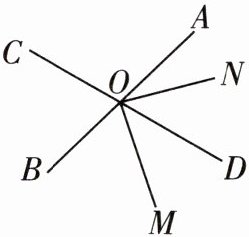
如图,直线$AB$,$CD相交于点O$,$ON把\angle AOD$分成两个角,且$\angle AON:\angle NOD= 2:3$。
【问题提出】
(1)若$\angle BOC= 75^{\circ}$,求$\angle AON$的度数。
(2)在(1)的基础上,若$OM平分\angle BON$,则$OB是\angle COM$的平分线吗?并说明理由。
【问题解决】
(3)若$OM\perp ON于点O$,则$\frac{3}{5}\angle AOC-\angle DOM$是否为固定度数?若是,请求出该度数;若不是,请说明理由。

答案:
解:
(1)因为∠AOD与∠BOC是对顶角,所以∠AOD=∠BOC=75°.因为∠AON:∠NOD=2:3,所以∠AON=2/5∠AOD=2/5×75°=30°.
(2)是.理由如下:根据
(1),得∠AON=30°,所以∠BON=180° - ∠AON=150°.因为OM平分∠BON,所以∠BOM=∠MON=75°,所以∠COB=∠BOM,所以OB是∠COM的平分线.
(3)是固定度数.理由如下:因为∠AON:∠NOD=2:3,所以∠NOD=3/2∠AON.因为OM⊥ON,所以∠MON=90°,所以∠DOM=90° - 3/2∠AON.因为∠AOD=∠AON+∠NOD=5/2∠AON,所以∠AOC=180° - ∠AOD=180° - 5/2∠AON,所以3/5∠AOC - ∠DOM=3/5(180° - 5/2∠AON)-(90° - 3/2∠AON)=18°.
(1)因为∠AOD与∠BOC是对顶角,所以∠AOD=∠BOC=75°.因为∠AON:∠NOD=2:3,所以∠AON=2/5∠AOD=2/5×75°=30°.
(2)是.理由如下:根据
(1),得∠AON=30°,所以∠BON=180° - ∠AON=150°.因为OM平分∠BON,所以∠BOM=∠MON=75°,所以∠COB=∠BOM,所以OB是∠COM的平分线.
(3)是固定度数.理由如下:因为∠AON:∠NOD=2:3,所以∠NOD=3/2∠AON.因为OM⊥ON,所以∠MON=90°,所以∠DOM=90° - 3/2∠AON.因为∠AOD=∠AON+∠NOD=5/2∠AON,所以∠AOC=180° - ∠AOD=180° - 5/2∠AON,所以3/5∠AOC - ∠DOM=3/5(180° - 5/2∠AON)-(90° - 3/2∠AON)=18°.
查看更多完整答案,请扫码查看


