第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
【问题背景】
素材 $1$ 每年秋天是灵昆柿子饼盛产期. 小黄同学打算从灵昆寄 $5$ 袋柿子饼到杭州,以每袋 $3$ kg 为标准,超过的千克数记为正数,不足的千克数记为负数,记录如下表所示:

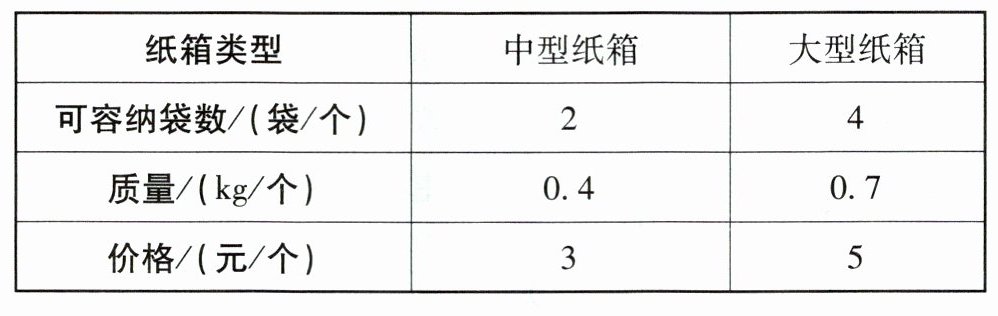
素材 $2$ 小黄同学选择了某快递,收费标准如下:$3$ kg 以内 $15$ 元(含 $3$ kg),超过 $3$ kg 的部分为 $2$ 元/kg(不足 $1$ kg 按 $1$ kg 计). 现该快递公司提供多种寄件包装方式(如表所示):
【方案设计】
方案一:小黄购买了中型纸箱将质量低的②④袋柿子饼打包在一起,其余每小袋不装纸箱各自寄出.
方案二:
【问题解决】
任务 $1$ 求这 $5$ 袋柿子饼的总质量.
任务 $2$ 求方案一所需要的总费用.
任务 $3$ 请你设计方案二,使它的费用低于方案一,并计算你的方案总费用.
素材 $1$ 每年秋天是灵昆柿子饼盛产期. 小黄同学打算从灵昆寄 $5$ 袋柿子饼到杭州,以每袋 $3$ kg 为标准,超过的千克数记为正数,不足的千克数记为负数,记录如下表所示:

素材 $2$ 小黄同学选择了某快递,收费标准如下:$3$ kg 以内 $15$ 元(含 $3$ kg),超过 $3$ kg 的部分为 $2$ 元/kg(不足 $1$ kg 按 $1$ kg 计). 现该快递公司提供多种寄件包装方式(如表所示):

【方案设计】
方案一:小黄购买了中型纸箱将质量低的②④袋柿子饼打包在一起,其余每小袋不装纸箱各自寄出.
方案二:
购买1个大型纸箱,将①,②,④,⑤打包一起邮寄,③单独邮寄
.【问题解决】
任务 $1$ 求这 $5$ 袋柿子饼的总质量.
任务 $2$ 求方案一所需要的总费用.
任务 $3$ 请你设计方案二,使它的费用低于方案一,并计算你的方案总费用.
答案:
任务1 由题意可知,$0.1+(-0.3)+0+(-0.1)+0.2=-0.1(kg)$,$5×3+(-0.1)=14.9(kg)$,故这5袋柿子饼的总质量为$14.9\ kg$.
任务2 第②,④袋柿子饼打包后总质量为$(-0.3)+(-0.1)+2×3+0.4=6(kg)$,故邮寄费用为$15+(6-3)×2+3=24(元)$.
第①袋柿子饼,$3+0.1=3.1\gt3$,故邮寄费用为$15+2=17(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
第⑤袋柿子饼,$3+0.2=3.2\gt3$,故邮寄费用为$15+2=17(元)$.
所以方案一所需要的总费用为$24+17+15+17=73(元)$.
任务3 答案不唯一,合理即可.
方案Ⅰ:购买1个大型纸箱,将①,②,④,⑤打包一起邮寄,③单独邮寄.
第①,②,④,⑤袋柿子饼打包后总质量为$0.1+(-0.3)+(-0.1)+0.2+4×3+0.7=12.6(kg)$,故邮寄费用为$15+10×2+5=40(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$40+15=55(元)$.
方案Ⅱ:购买2个中型纸箱,分别将①④,②⑤打包一起邮寄,③单独邮寄.
第①,④袋柿子饼打包后总质量为$0.1+(-0.1)+2×3+0.4=6.4(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第②,⑤袋柿子饼打包后总质量为$(-0.3)+0.2+2×3+0.4=6.3(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$26+26+15=67(元)$.
方案Ⅲ:购买2个中型纸箱,分别将②④,①⑤打包一起邮寄,③单独邮寄.
由【任务2】可知第②,④袋柿子饼邮寄费用为$24\ 元$.
第①,⑤袋柿子饼打包后总质量为$0.1+0.2+2×3+0.4=6.7(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$24+26+15=65(元)$.
任务2 第②,④袋柿子饼打包后总质量为$(-0.3)+(-0.1)+2×3+0.4=6(kg)$,故邮寄费用为$15+(6-3)×2+3=24(元)$.
第①袋柿子饼,$3+0.1=3.1\gt3$,故邮寄费用为$15+2=17(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
第⑤袋柿子饼,$3+0.2=3.2\gt3$,故邮寄费用为$15+2=17(元)$.
所以方案一所需要的总费用为$24+17+15+17=73(元)$.
任务3 答案不唯一,合理即可.
方案Ⅰ:购买1个大型纸箱,将①,②,④,⑤打包一起邮寄,③单独邮寄.
第①,②,④,⑤袋柿子饼打包后总质量为$0.1+(-0.3)+(-0.1)+0.2+4×3+0.7=12.6(kg)$,故邮寄费用为$15+10×2+5=40(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$40+15=55(元)$.
方案Ⅱ:购买2个中型纸箱,分别将①④,②⑤打包一起邮寄,③单独邮寄.
第①,④袋柿子饼打包后总质量为$0.1+(-0.1)+2×3+0.4=6.4(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第②,⑤袋柿子饼打包后总质量为$(-0.3)+0.2+2×3+0.4=6.3(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$26+26+15=67(元)$.
方案Ⅲ:购买2个中型纸箱,分别将②④,①⑤打包一起邮寄,③单独邮寄.
由【任务2】可知第②,④袋柿子饼邮寄费用为$24\ 元$.
第①,⑤袋柿子饼打包后总质量为$0.1+0.2+2×3+0.4=6.7(kg)$,故邮寄费用为$15+4×2+3=26(元)$.
第③袋柿子饼,$3+0=3(kg)$,故邮寄费用为$15\ 元$.
该方案所需要的总费用为$24+26+15=65(元)$.
查看更多完整答案,请扫码查看


