第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
1 当 $ a = -2 $ 时,代数式 $ 2a + 2 $ 的值是 (
A.$-6$
B.$-2$
C.$0$
D.$4$
B
)A.$-6$
B.$-2$
C.$0$
D.$4$
答案:
B 因为a=-2,所以2a+2=2×(-2)+2=-4+2=-2.
2 当 $ a = 2 $,$ b = -3 $ 时,代数式 $ (a - b)^2 + 2ab $ 的值为 (
A.$13$
B.$27$
C.$-5$
D.$-7$
13
)A.$13$
B.$27$
C.$-5$
D.$-7$
答案:
A 当a=2,b=-3时,(a-b)²+2ab=[2-(-3)]²+2×2×(-3)=13.
3 下表表示对每个 $ x $ 的取值,某个代数式的相应的值,则满足表中所列所有条件的代数式是(
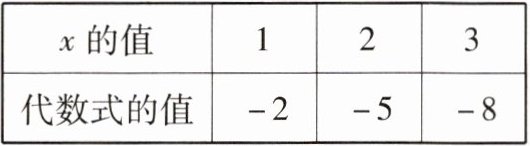
A.$ x - 3 $
B.$ 2x - 10 $
C.$ 3x - 17 $
D.$ -3x + 1 $
D
)
A.$ x - 3 $
B.$ 2x - 10 $
C.$ 3x - 17 $
D.$ -3x + 1 $
答案:
D 当x=2,3时,x-3的值分别为-1,0,故选项A不符合题意(找到一个不符合要求的即可排除该选项);当x=1,代数式的值2,3时,2x-10的值分别是-8,-6,-4,故选项B不符合题意;当x=1,2,3时,3x-17的值分别是-14,-11,-8,故选项C不符合题意.将x的值分别代入选项D中的代数式,所得代数式的值均满足要求,所以选项D符合题意.
4 若 $ |a - 6| + |b - 3| = 0 $,则 $ a^2 - b^3 $ 的值为
9
。
答案:
9 因为|a-6|+|b-3|=0,所以a-6=0,b-3=0(绝对值的非负性),所以a=6,b=3,所以a²-b³=6²-3³=36-27=9.
5 新情境 现代营养学家用身体质量指数 $ p $ 衡量人体胖瘦程度,这个指数等于“人体体重 $ w(kg) $”与“人体身高 $ h(m) $ 的平方”的商,即 $ p = \frac{w}{h^2} $。若张宇(成年人)的身高是 $ 1.80 m $,体重是 $ 81 kg $,他的体重属于
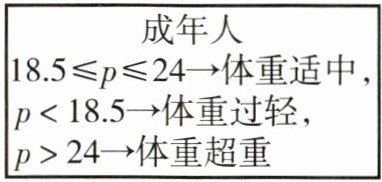
超重
。(填“过轻”“适中”或“超重”)
答案:
超重 当w=81,h=1.80时,p=81/1.80²=25>24,所以张宇的体重超重.
6 跨学科·物理 [2024 广州中考] 如图,把 $ R_1 $,$ R_2 $,$ R_3 $ 三个电阻串联起来,线路 $ AB $ 上的电流为 $ I $,电压为 $ U $,则 $ U = IR_1 + IR_2 + IR_3 $。当 $ R_1 = 20.3 $,$ R_2 = 31.9 $,$ R_3 = 47.8 $,$ I = 2.2 $ 时,$ U $ 的值为

220
。
答案:
220 已知U=IR₁+IR₂+IR₃,当R₁=20.3,R₂=31.9,R₃=47.8,I=2.2时,U=20.3×2.2+31.9×2.2+47.8×2.2=(20.3+31.9+47.8)×2.2=220.
7 [2025 汕头期末] 当 $ x = 1 $ 时,$ px^3 + qx + 1 = 2024 $,则当 $ x = -1 $ 时,$ px^3 + qx - 1 $ 的值为 (
A.$ 2025 $
B.$ -2025 $
C.$ 2024 $
D.$ -2024 $
D
)A.$ 2025 $
B.$ -2025 $
C.$ 2024 $
D.$ -2024 $
答案:
D 根据题意,得p+q+1=2024,所以p+q=2023,所以当x=-1时,px³+qx-1=-(p+q)(整体代入)-1=-2023-1=-2024.
8 [2025 苏州段考] 按如图所示的程序计算,若开始输入 $ x = 3 $,则最后输出的结果是 (
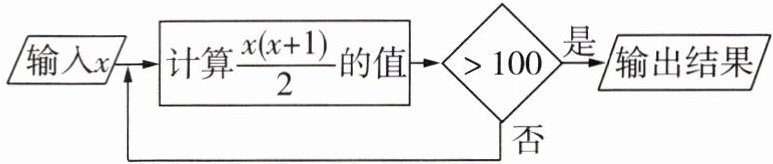
A.$6$
B.$21$
C.$156$
D.$231$
D
)
A.$6$
B.$21$
C.$156$
D.$231$
答案:
D 根据题意,得当x=3时,x(x+1)/2=6<100;当x=6时,x(x+1)/2=21<100;当x=21时,x(x+1)/2=231>100,所以最后输出的结果是231.
9 [2024 广州中考] 若 $ a^2 - 2a - 5 = 0 $,则 $ 2a^2 - 4a + 1 = $
11
。
答案:
11 因为a²-2a-5=0,所以a²-2a=5,所以2a²-4a+1=2(a²-2a)(整体代入)+1=2×5+1=11.
10 [2025 眉山期末] 已知 $ a $,$ b $ 互为相反数,$ c $,$ d $ 互为倒数,$ |m| = 3 $,求 $ \frac{a + b}{m} - cd + m + 2025 $ 的值。
答案:
解:因为a,b互为相反数,c,d互为倒数,|m|=3,所以a+b=0,cd=1,m=±3.①当m=3时,(a+b)/m -cd+m+2025=0/3 -1+3+2025=2027.②当m=-3时,(a+b)/m -cd+m+2025=0/(-3)-1-3+2025=2021.综上,(a+b)/m -cd+m+2025的值为2027或2021.
11 推理能力 [2024 重庆中考 B 卷] 用菱形按如图所示的规律拼图案,其中第①个图案中有 $ 2 $ 个菱形,第②个图案中有 $ 5 $ 个菱形,第③个图案中有 $ 8 $ 个菱形,第④个图案中有 $ 11 $ 个菱形,…,按此规律,则第⑧个图案中,菱形的个数是 (
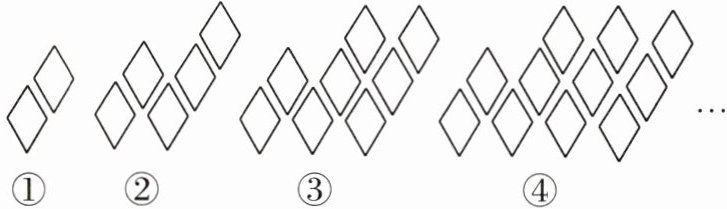
A.$20$
B.$21$
C.$23$
D.$26$
23
)
A.$20$
B.$21$
C.$23$
D.$26$
答案:
C 题中第①个图案中有1×3-1=2(个)菱形,第②个图案中有2×3-1=5(个)菱形,第③个图案中有3×3-1=8(个)菱形,第④个图案中有4×3-1=11(个)菱形……第n个图案中有n×3-1=(3n-1)个菱形,所以第⑧个图案中菱形的个数为3×8-1=23.
查看更多完整答案,请扫码查看


