第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
1 [2025 杭州期末]【特例感知】
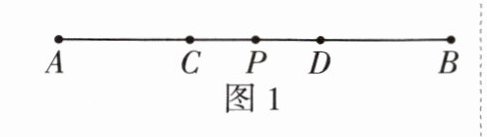
(1)如图 1,P 为线段 AB 的中点,点 C,D 把线段 AB 三等分. 若 AB = 12 cm,求 CP 的长.
【知识迁移】
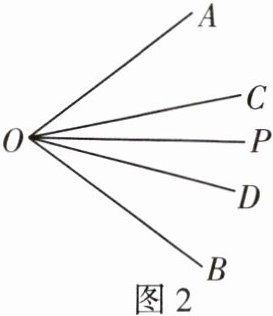
(2)如图 2,射线 OP 平分∠AOB,射线 OC,OD 把∠AOB 三等分. 若∠COP = θ,求∠AOB 的度数. (用含θ的式子表示)
(1)如图 1,P 为线段 AB 的中点,点 C,D 把线段 AB 三等分. 若 AB = 12 cm,求 CP 的长.

【知识迁移】
(2)如图 2,射线 OP 平分∠AOB,射线 OC,OD 把∠AOB 三等分. 若∠COP = θ,求∠AOB 的度数. (用含θ的式子表示)

答案:
1 解:
(1)根据题意,得
$AP=BP=\frac{1}{2}AB=\frac{1}{2}×12=6(cm),$
$AC=CD=BD=\frac{1}{3}AB=\frac{1}{3}×12=4(cm),$
所以 CP=AP-AC=6-4=2(cm).
(2)因为射线 OP 平分∠AOB,
所以$∠BOP=∠AOP=\frac{1}{2}∠AOB.$
因为射线 OC,OD 把∠AOB 三等分,
所以$∠AOC=∠COD=∠BOD=\frac{1}{3}∠AOB,$
所以∠AOP-∠AOC=∠BOP-∠BOD,
所以∠COP=∠DOP=θ,所以∠COD=2θ,
所以∠AOB=3∠COD=6θ.
(1)根据题意,得
$AP=BP=\frac{1}{2}AB=\frac{1}{2}×12=6(cm),$
$AC=CD=BD=\frac{1}{3}AB=\frac{1}{3}×12=4(cm),$
所以 CP=AP-AC=6-4=2(cm).
(2)因为射线 OP 平分∠AOB,
所以$∠BOP=∠AOP=\frac{1}{2}∠AOB.$
因为射线 OC,OD 把∠AOB 三等分,
所以$∠AOC=∠COD=∠BOD=\frac{1}{3}∠AOB,$
所以∠AOP-∠AOC=∠BOP-∠BOD,
所以∠COP=∠DOP=θ,所以∠COD=2θ,
所以∠AOB=3∠COD=6θ.
2 [2025 济南天桥区月考]【特例感知】
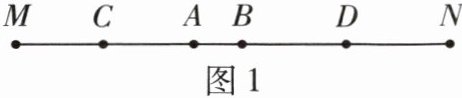
(1)如图 1,MN = 27 cm,AB = 3 cm,线段 AB 在线段 MN 上运动,点 C,D 分别是 AM,BN 的中点. 若 AM = 16 cm,求 CD 的长.
【知识迁移】
(2)在(1)的条件下,当 AB 运动时,CD 的长度是否发生变化?若不变,求 CD 的长;若变化,请说明理由.
【拓展探究】
(3)角的很多规律和线段一样,如图 2,已知∠AOB 在∠MON 内转动,射线 OC 和 OD 分别平分∠AOM 和∠BON. 若∠MON = 160°,∠AOB = 30°,求∠COD 的度数.

追问:∠AOB,∠COD 和∠MON 之间的数量关系为______.
(1)因为 MN=27 cm,AB=3 cm,AM=16 cm,
所以 BN=MN-AB-AM=8 cm.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM=8 cm,BD=\frac{1}{2}BN=4 cm,$
所以 CD=AC+AB+BD=8+3+4=15(cm).
(2)不变.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM,BD=\frac{1}{2}BN,$
所以$ AC+BD=\frac{1}{2}AM+\frac{1}{2}BN=\frac{1}{2}(AM+BN).$
因为 MN=27 cm,AB=3 cm,
所以 AM+BN=MN-AB=27-3=24(cm),
所以$ AC+BD=\frac{1}{2}(AM+BN)=12 cm,$
所以 CD=AC+AB+BD=12+3=15(cm).
(3)因为 OC 和 OD 分别平分∠AOM 和∠BON,
所以$∠AOC=\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$
所以$∠AOC+∠BOD=\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON).$
因为∠MON=160°,∠AOB=30°,
所以∠AOM+∠BON=∠MON-∠AOB=130°,
所以∠AOC+∠BOD=65°,
所以∠COD=∠AOC+∠BOD+∠AOB=65°+30°=95°.
追问$:∠COD=\frac{1}{2}(∠MON+∠AOB)$
(1)如图 1,MN = 27 cm,AB = 3 cm,线段 AB 在线段 MN 上运动,点 C,D 分别是 AM,BN 的中点. 若 AM = 16 cm,求 CD 的长.

【知识迁移】
(2)在(1)的条件下,当 AB 运动时,CD 的长度是否发生变化?若不变,求 CD 的长;若变化,请说明理由.
【拓展探究】
(3)角的很多规律和线段一样,如图 2,已知∠AOB 在∠MON 内转动,射线 OC 和 OD 分别平分∠AOM 和∠BON. 若∠MON = 160°,∠AOB = 30°,求∠COD 的度数.

追问:∠AOB,∠COD 和∠MON 之间的数量关系为______.
(1)因为 MN=27 cm,AB=3 cm,AM=16 cm,
所以 BN=MN-AB-AM=8 cm.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM=8 cm,BD=\frac{1}{2}BN=4 cm,$
所以 CD=AC+AB+BD=8+3+4=15(cm).
(2)不变.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM,BD=\frac{1}{2}BN,$
所以$ AC+BD=\frac{1}{2}AM+\frac{1}{2}BN=\frac{1}{2}(AM+BN).$
因为 MN=27 cm,AB=3 cm,
所以 AM+BN=MN-AB=27-3=24(cm),
所以$ AC+BD=\frac{1}{2}(AM+BN)=12 cm,$
所以 CD=AC+AB+BD=12+3=15(cm).
(3)因为 OC 和 OD 分别平分∠AOM 和∠BON,
所以$∠AOC=\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$
所以$∠AOC+∠BOD=\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON).$
因为∠MON=160°,∠AOB=30°,
所以∠AOM+∠BON=∠MON-∠AOB=130°,
所以∠AOC+∠BOD=65°,
所以∠COD=∠AOC+∠BOD+∠AOB=65°+30°=95°.
追问$:∠COD=\frac{1}{2}(∠MON+∠AOB)$
答案:
2 解:
(1)因为 MN=27 cm,AB=3 cm,AM=16 cm,
所以 BN=MN-AB-AM=8 cm.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM=8 cm,BD=\frac{1}{2}BN=4 cm,$
所以 CD=AC+AB+BD=8+3+4=15(cm).
(2)不变.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM,BD=\frac{1}{2}BN,$
所以$ AC+BD=\frac{1}{2}AM+\frac{1}{2}BN=\frac{1}{2}(AM+BN).$
因为 MN=27 cm,AB=3 cm,
所以 AM+BN=MN-AB=27-3=24(cm),
所以$ AC+BD=\frac{1}{2}(AM+BN)=12 cm,$
所以 CD=AC+AB+BD=12+3=15(cm).
(3)因为 OC 和 OD 分别平分∠AOM 和∠BON,
所以$∠AOC=\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$
所以$∠AOC+∠BOD=\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON).$
因为∠MON=160°,∠AOB=30°,
所以∠AOM+∠BON=∠MON-∠AOB=130°,
所以∠AOC+∠BOD=65°,
所以∠COD=∠AOC+∠BOD+∠AOB=65°+30°=95°.
追问$:∠COD=\frac{1}{2}(∠MON+∠AOB)$
因为 OC 和 OD 分别平分∠AOM 和∠BON,所以∠AOC=
$\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$所以∠AOC+∠BOD=
$\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON),$所以∠COD=
$∠AOC+∠BOD+∠AOB=\frac{1}{2}(∠AOM+∠BON)+∠AOB=$
$\frac{1}{2}(∠MON-∠AOB)+∠AOB=\frac{1}{2}(∠MON+∠AOB).$
(1)因为 MN=27 cm,AB=3 cm,AM=16 cm,
所以 BN=MN-AB-AM=8 cm.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM=8 cm,BD=\frac{1}{2}BN=4 cm,$
所以 CD=AC+AB+BD=8+3+4=15(cm).
(2)不变.
因为点 C,D 分别是 AM,BN 的中点,
所以$ AC=\frac{1}{2}AM,BD=\frac{1}{2}BN,$
所以$ AC+BD=\frac{1}{2}AM+\frac{1}{2}BN=\frac{1}{2}(AM+BN).$
因为 MN=27 cm,AB=3 cm,
所以 AM+BN=MN-AB=27-3=24(cm),
所以$ AC+BD=\frac{1}{2}(AM+BN)=12 cm,$
所以 CD=AC+AB+BD=12+3=15(cm).
(3)因为 OC 和 OD 分别平分∠AOM 和∠BON,
所以$∠AOC=\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$
所以$∠AOC+∠BOD=\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON).$
因为∠MON=160°,∠AOB=30°,
所以∠AOM+∠BON=∠MON-∠AOB=130°,
所以∠AOC+∠BOD=65°,
所以∠COD=∠AOC+∠BOD+∠AOB=65°+30°=95°.
追问$:∠COD=\frac{1}{2}(∠MON+∠AOB)$
因为 OC 和 OD 分别平分∠AOM 和∠BON,所以∠AOC=
$\frac{1}{2}∠AOM,∠BOD=\frac{1}{2}∠BON,$所以∠AOC+∠BOD=
$\frac{1}{2}∠AOM+\frac{1}{2}∠BON=\frac{1}{2}(∠AOM+∠BON),$所以∠COD=
$∠AOC+∠BOD+∠AOB=\frac{1}{2}(∠AOM+∠BON)+∠AOB=$
$\frac{1}{2}(∠MON-∠AOB)+∠AOB=\frac{1}{2}(∠MON+∠AOB).$
查看更多完整答案,请扫码查看


