第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
11 [2025绍兴期末]按如图所示的方法折纸,下列说法不一定正确的是 (
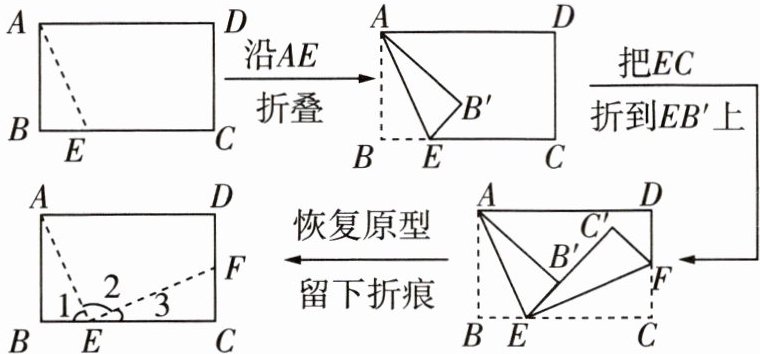
A.$∠2 = ∠1 + ∠3$
B.$∠1与∠3$互余
C.$∠1与∠AEC$互补
D.$EC'平分∠AEF$
D
)
A.$∠2 = ∠1 + ∠3$
B.$∠1与∠3$互余
C.$∠1与∠AEC$互补
D.$EC'平分∠AEF$
答案:
D 根据折叠的性质可知,∠1=∠AEB',∠3=∠FEC',所以∠2=∠1+∠3.因为∠1+∠AEB'+∠3+∠FEC'=180°,∠AEB'+∠FEC'=∠2,所以∠2+∠1+∠3=180°,所以∠1+∠3=90°,即∠1与∠3互余.因为点E在BC上,所以∠1+∠AEC=180°,所以∠1与∠AEC互补.根据题中条件无法得到∠1=∠3,所以无法得到EC'平分∠AEF.
12 [2025南京外国语学校月考]如图,点$C是射线OA$上一点,过点$C作CD ⊥ OB于点D$,作$CE ⊥ OA于点C$,则下列错误的是 (
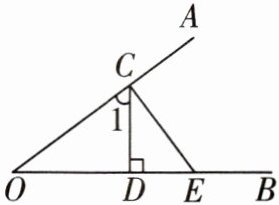
A.$∠1是∠ECD$的余角
B.$∠AOB = ∠DCE$
C.图中互余的角共有3对
D.$∠ACD = ∠BEC$
C
)
A.$∠1是∠ECD$的余角
B.$∠AOB = ∠DCE$
C.图中互余的角共有3对
D.$∠ACD = ∠BEC$
答案:
C 因为CE⊥OA,所以∠OCE=90°,所以∠ECD+∠1=90°,所以∠1与∠ECD互余,选项A正确.因为CD⊥OB,所以∠CDO=∠CDE=90°,所以∠DCE+∠OEC=90°.因为∠AOB+∠OEC=90°,所以∠AOB=∠DCE,选项B正确.因为∠1+∠AOB=∠1+∠DCE=∠DCE+∠CED=∠AOB+∠CED=90°,所以题图中共有4对角互余,选项C错误.因为∠1+∠DCE=90°,∠CED+∠DCE=90°,所以∠1=∠CED.因为∠ACD+∠1=180°,∠BEC+∠CED=180°,所以∠ACD=∠BEC,选项D正确.
13 若$∠α与∠β$互补,且$∠α > ∠β$,给出下列式子:①$90° - ∠β$;②$∠α - 90°$;③$180° - ∠α$;④$\frac{1}{2}(∠α - ∠β)$. 其中是$∠β$的余角的是
①②④
.(填序号)
答案:
①②④ 因为∠α与∠β互补,所以∠α+∠β=180°,所以∠β=180°-∠α,所以90°-∠β=90°-(180°-∠α)=90°-180°+∠α=∠α-90°,所以∠α-90°是∠β的余角;因为$\frac{1}{2}$(∠α-∠β)=$\frac{1}{2}$(180°-∠β-∠β)=$\frac{1}{2}$(180°-2∠β)=90°-∠β,所以$\frac{1}{2}$(∠α-∠β)是∠β的余角.所以①②④是∠β的余角.
14 推理能力已知$α$,$β$都是锐角,$γ$是钝角.
(1)在计算$\frac{1}{3}(α + β + γ)$的度数时,有三位同学分别算出了$119°$,$120°$,$121°$,这三个不同的结果,只有一个是正确答案,请你求$α + β + γ$的值;
(2)在(1)的情况下,若锐角$β比锐角α小1°$,钝角$γ是锐角α$的2倍,求$γ$的补角的度数.
(1)在计算$\frac{1}{3}(α + β + γ)$的度数时,有三位同学分别算出了$119°$,$120°$,$121°$,这三个不同的结果,只有一个是正确答案,请你求$α + β + γ$的值;
(2)在(1)的情况下,若锐角$β比锐角α小1°$,钝角$γ是锐角α$的2倍,求$γ$的补角的度数.
答案:
(1)因为α,β都是锐角,γ是钝角, 所以α+β+γ<360°. 若$\frac{1}{3}$(α+β+γ)=119°,则α+β+γ=357°,符合题意; 若$\frac{1}{3}$(α+β+γ)=120°,则α+β+γ=360°,不符合题意; 若$\frac{1}{3}$(α+β+γ)=121°,则α+β+γ=363°,不符合题意; 综上,α+β+γ=357°.
(2)由题知β=α-1,γ=2α.因为α+β+γ=357°, 所以α+α-1+2α=357°, 所以α=89.5°,所以γ=2α=179°, 所以γ的补角的度数是180°-179°=1°.
(1)因为α,β都是锐角,γ是钝角, 所以α+β+γ<360°. 若$\frac{1}{3}$(α+β+γ)=119°,则α+β+γ=357°,符合题意; 若$\frac{1}{3}$(α+β+γ)=120°,则α+β+γ=360°,不符合题意; 若$\frac{1}{3}$(α+β+γ)=121°,则α+β+γ=363°,不符合题意; 综上,α+β+γ=357°.
(2)由题知β=α-1,γ=2α.因为α+β+γ=357°, 所以α+α-1+2α=357°, 所以α=89.5°,所以γ=2α=179°, 所以γ的补角的度数是180°-179°=1°.
1 在同一条直线上有三个点 A,B,C. 若 AB = 10 cm,AC = 30 cm,点 M 是 AB 的中点,点 N 是 AC 的中点,求线段 MN 的长.
答案:
解:如图1,当点B在线段AC上时,
MN=AN - AM = $\frac{1}{2}$AC - $\frac{1}{2}$AB = 15 - 5 = 10(cm).
如图2,当点B在线段AC的反向延长线上时,
MN=AN + AM = $\frac{1}{2}$AC + $\frac{1}{2}$AB = 15 + 5 = 20(cm).
综上,线段MN的长为10cm或20cm.
MN=AN - AM = $\frac{1}{2}$AC - $\frac{1}{2}$AB = 15 - 5 = 10(cm).
如图2,当点B在线段AC的反向延长线上时,
MN=AN + AM = $\frac{1}{2}$AC + $\frac{1}{2}$AB = 15 + 5 = 20(cm).
综上,线段MN的长为10cm或20cm.
2 定义:有一条公共边的两个互余的角叫做“友余角”. 已知 ∠α 和 ∠β 为一对“友余角”,∠α = 20°,求 ∠α 的平分线和 ∠β 的平分线所成的角的度数.
答案:
解:因为∠α和∠β为一对“友余角”,∠α = 20°,
所以∠β = 90° - 20° = 70°.
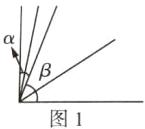
如图1,当∠α在∠β的外部时,
∠α和∠β的平分线所成的角的度数是$\frac{1}{2}$∠α + $\frac{1}{2}$∠β = 45°.
如图2,当∠α在∠β的内部时,
∠α和∠β的平分线所成的角的度数是$\frac{1}{2}$∠β - $\frac{1}{2}$∠α = 25°.
综上,∠α和∠β的平分线所成的角的度数为45°或25°.

解:因为∠α和∠β为一对“友余角”,∠α = 20°,
所以∠β = 90° - 20° = 70°.
如图1,当∠α在∠β的外部时,
∠α和∠β的平分线所成的角的度数是$\frac{1}{2}$∠α + $\frac{1}{2}$∠β = 45°.
如图2,当∠α在∠β的内部时,
∠α和∠β的平分线所成的角的度数是$\frac{1}{2}$∠β - $\frac{1}{2}$∠α = 25°.
综上,∠α和∠β的平分线所成的角的度数为45°或25°.


查看更多完整答案,请扫码查看


