《2025年一遍过七年级数学上册华师大版》

12. 若规定乘积为 -1 的两个数互为负倒数,则 -2 的负倒数是(C)
A.-2
B.$-\frac{1}{2}$
C.$\frac{1}{2}$
D.2

答案： C

13. [2025 汕尾期末]有理数 a,b 在数轴上的位置如图所示,则下列结论正确的是(A)

A.$b - a ＞ 0$
B.$a + b ＞ 0$
C.$ab ＞ 0$
D.$\frac{a}{b} ＞ 0$

答案： A 根据题中数轴可得,$a＜-1＜0＜b＜1$且$|a|＞|b|$,所以$b-a＞0$,$a+b＜0$,$ab＜0$,$\frac{a}{b}＜0$.

14. 若 a,b 均是非 0 的自然数,则$\frac{1}{a}÷b$=$\frac{1}{b}÷a$。(填“＞”“＜”或“=”)

答案： = $\frac{1}{a}÷ b=\frac{1}{a}×\frac{1}{b}=\frac{1}{ab}$,$\frac{1}{b}÷ a=\frac{1}{b}×\frac{1}{a}=\frac{1}{ab}$,即两者相等.

15. [2025 南京鼓楼区求真中学月考]从 -5,-3,-1,2,4 中任取 2 个数,所得积的最大值记为 a,所得商的最小值记为 b,则$\frac{a}{b}$的值为$-\frac{15}{4}$。

答案： $-\frac{15}{4}$ 易知最大值$a=-5×(-3)=15$,最小值$b=\frac{4}{-1}=-4$,所以$\frac{a}{b}=\frac{15}{-4}=-\frac{15}{4}$.

16. [新趋势·过程性学习][教材 P53 练习 T3 变式]下面是小胡同学的解题过程：

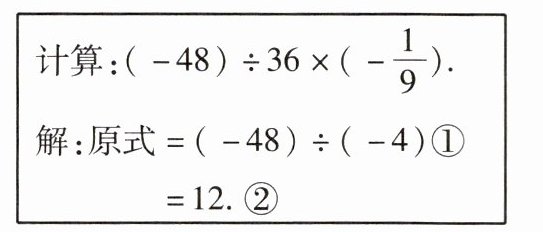
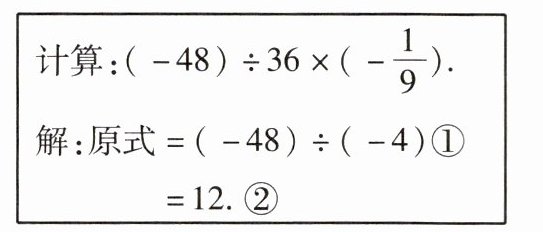
(1) 上述解题过程,从第①步开始出错(填序号),原因是没有按从左到右的顺序计算；
(2) 请你写出正确的解答过程。
解:$(-48)÷36×(-\frac{1}{9})=-\frac{4}{3}×(-\frac{1}{9})=\frac{4}{27}$.

答案：
(1)① 没有按从左到右的顺序计算
(2)请你写出正确的解答过程。解:$(-48)÷36×(-\frac{1}{9})=-\frac{4}{3}×(-\frac{1}{9})=\frac{4}{27}$.

17. 计算：$(-5)÷(-1\frac{2}{7})÷1\frac{1}{4}×(-2\frac{1}{4})÷7$。

答案： 解:$(-5)÷(-1\frac{2}{7})÷1\frac{1}{4}×(-2\frac{1}{4})÷7=-5×\frac{7}{9}×\frac{4}{5}×\frac{9}{4}×\frac{1}{7}=-1$.

18. [2025 长沙开福区立信中学月考]已知 a,b 互为倒数,c,d 互为相反数(c,d 均不为 0),$|m| = 3$。
(1) $ab = $1,$c + d = $0,$m = $±3,$\frac{c}{d} = $-1；
(2) 求$\frac{m}{3} + ab + \frac{c + d}{4m} - \frac{c}{d}$的值。
解:当$m=3$时,$\frac{m}{3}+ab+\frac{c+d}{4m}-\frac{c}{d}=1+1+0-(-1)=3$;当$m=-3$时,$\frac{m}{3}+ab+\frac{c+d}{4m}-\frac{c}{d}=-1+1+0-(-1)=1$

答案：
(1)1 0 ±3 -1
(2)求$\frac{m}{3} + ab + \frac{c + d}{4m} - \frac{c}{d}$的值。解:当$m=3$时,$\frac{m}{3}+ab+\frac{c+d}{4m}-\frac{c}{d}=1+1+0-(-1)=3$;当$m=-3$时,$\frac{m}{3}+ab+\frac{c+d}{4m}-\frac{c}{d}=-1+1+0-(-1)=1$.

19. [2025 安阳期中]某景区山脚的地面温度为$18^{\circ}C$,据气象观测资料表明,该地的海拔每增加 1 km,气温大约下降$6^{\circ}C$。
(1) 求海拔 3 km 处的温度；
(2) 若山上某处的气温为$-12^{\circ}C$,求此处的海拔。

答案：
(1)求海拔 3 km 处的温度；解:根据题意,得海拔3 km处的温度是$18+(-6)×3=0(^{\circ}C)$.
(2)若山上某处的气温为$-12^{\circ}C$,求此处的海拔。解:此处的海拔为$[(-12)-18]÷(-6)=5(km)$.

20. [运算能力]已知$|x| = \begin{cases} x(x ＞ 0), \\ 0(x = 0), \\ -x(x ＜ 0), \end{cases} 即当x ＜ 0$时,$\frac{x}{|x|} = \frac{x}{-x} = -1$。
(1) 已知 a,b 是有理数。
① 当$a ＞ 0$,$b ＞ 0$时,$\frac{a}{|a|} + \frac{b}{|b|} = $2；
② 当$a ＞ 0$,$b ＜ 0$时,$\frac{a}{|a|} + \frac{b}{|b|} = $0；
③ 当$a ＜ 0$,$b ＜ 0$时,$\frac{a}{|a|} + \frac{b}{|b|} = $-2。
(2) 已知 a,b,c 是有理数,当$abc ＜ 0$时,求$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|}$的值。
当$abc＜0$时，分以下情况讨论：①当$a＜0,b＜0,c＜0$时，$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=\frac{a}{-a}+\frac{b}{-b}+\frac{c}{-c}=-1-1-1=-3$。②当$a＜0,b＞0,c＞0$时，$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=\frac{a}{-a}+\frac{b}{b}+\frac{c}{c}=-1+1+1=1$。同理，当$a＞0,b＜0,c＞0$或$a＞0,b＞0,c＜0$时，$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=1$。综上，$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$的值为-3或1。

答案： 解题思路:
(2)当$abc＜0$时,$a,b,c$中有1个或有3个为负数,即分如下情况讨论:①$a＜0,b＜0,c＜0$,②$a＜0,b＞0,c＞0$(或$a＞0,b＜0,c＞0$或$a＞0,b＞0,c＜0$)解:
(1)①2;②0;③-2①因为$a＞0,b＞0$,所以$|a|=a$,$|b|=b$,所以$\frac{a}{|a|}+\frac{b}{|b|}=\frac{a}{a}+\frac{b}{b}=1+1=2$.②因为$a＞0,b＜0$,所以$|a|=a$,$|b|=-b$,所以$\frac{a}{|a|}+\frac{b}{|b|}=\frac{a}{a}+\frac{b}{-b}=1-1=0$.③因为$a＜0,b＜0$,所以$|a|=-a$,$|b|=-b$,所以$\frac{a}{|a|}+\frac{b}{|b|}=\frac{a}{-a}+\frac{b}{-b}=-1-1=-2$.
(2)当$abc＜0$时,分以下情况讨论:①当$a＜0,b＜0,c＜0$时,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=\frac{a}{-a}+\frac{b}{-b}+\frac{c}{-c}=-1-1-1=-3$.②当$a＜0,b＞0,c＞0$时,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=\frac{a}{-a}+\frac{b}{b}+\frac{c}{c}=-1+1+1=1$.同理,当$a＞0,b＜0,c＞0$或$a＞0,b＞0,c＜0$时,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=1$.综上,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$的值为-3或1.

[回顾与思考]有理数的加法与减法、乘法与除法各有什么关系？有理数的混合运算都能转化为加法与乘法运算吗？

答案： 有理数的减法是加法的逆运算，除法是乘法的逆运算；能转化为加法与乘法运算。