《2025年一遍过七年级数学上册华师大版》

6 新趋势·传统文化[2025合肥四十五中月考]我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量。如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如$2513= 2×7^{3}+5×7^{2}+1×7^{1}+3$)用来记录孩子出生的天数,由图可知,孩子出生的天数是______。

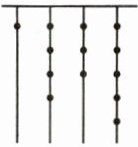
565

答案： 565 $1×7^{3}+4×7^{2}+3×7^{1}+5=1×343+4×49+3×7+5=565$,所以孩子出生的天数是565.

7 新考法 新趋势·结论开放[2025深圳期中]从一副扑克牌(去掉大、小王)中任意抽取四张,根据牌面上的数进行混合运算(包括加、减、乘、除和乘方),每一张牌必须用一次且只能用一次,可以加括号,使得运算结果为24或$-24$,其中黑色扑克牌代表正数(黑桃、梅花为黑色),红色扑克牌代表负数(红桃、方块为红色),A,J,Q,K分别代表1,11,12,13。比如,小明抽到了黑桃7,黑桃3,红桃3,梅花7,他运用下面的方法凑成了$7×[3-(-3)÷7]= 24$。若抽到的是黑桃A,红桃2,黑桃2,梅花3,则列出算式为$2^{3}×[1-(-2)]=24$(答案不唯一)。

答案： $2^{3}×[1-(-2)]=24$(答案不唯一)$2^{3}×[1-(-2)]=24$或$2^{3}×(-2-1)=-24$或$(-2)^{3}×(2+1)=-24$或$[3-(-2)]^{2}-1=24.$

8 用简便方法计算：$5×(-\frac{3}{7})-(-9)×(-\frac{2}{3})+(-5)×\frac{4}{7}$。

答案： 解:$5×(-\frac {3}{7})-(-9)×(-\frac {2}{3})+(-5)×\frac {4}{7}$$=5×(-\frac {3}{7})+5×(-\frac {4}{7})-(-9)×(-\frac {2}{3})$$=5×(-\frac {3}{7}-\frac {4}{7})-(-9)×(-\frac {2}{3})$$=-5-6=-11.$

9 新趋势·过程性学习 计算$50÷(\frac{1}{3}-\frac{1}{4}+\frac{1}{12})$,下面给出了三种不同的解法：
解法一 原式$=50÷\frac{1}{3}-50÷\frac{1}{4}+50÷\frac{1}{12}= 50×3-50×4+50×12= 550$。
解法二 原式$=50÷(\frac{4}{12}-\frac{3}{12}+\frac{1}{12})= 50÷\frac{2}{12}= 50×6= 300$。
解法三 原式的倒数为$(\frac{1}{3}-\frac{1}{4}+\frac{1}{12})÷50= (\frac{1}{3}-\frac{1}{4}+\frac{1}{12})×\frac{1}{50}= \frac{1}{3}×\frac{1}{50}-\frac{1}{4}×\frac{1}{50}+\frac{1}{12}×\frac{1}{50}= \frac{1}{300}$,所以原式$=300$。
(1)上述解法计算的结果不同,你认为哪个解法是错误的？并说明理由。
(2)请你选择两种合适的解法计算$(-\frac{1}{42})÷(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})$。

答案：
(1)解法一是错误的,原因是除法没有分配律.
(2)逆解 $(-\frac {1}{42})÷(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})=(-\frac {1}{42})÷(\frac {7}{42}-\frac {9}{42}+\frac {28}{42}-\frac {12}{42})=(-\frac {1}{42})÷\frac {7-9+28-12}{42}=-\frac {1}{42}×\frac {42}{14}=-\frac {1}{14}.$另解 $(-\frac {1}{42})÷(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})$的倒数为$(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})÷(-\frac {1}{42}),$$(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})÷(-\frac {1}{42})=(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})×(-42)=\frac {1}{6}×(-42)-\frac {3}{14}×(-42)+\frac {2}{3}×(-42)-\frac {2}{7}×(-42)=-14,$所以$(-\frac {1}{42})÷(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})=-\frac {1}{14}.$

10 应用意识[2025长春外国语学校月考]近几年,我国新能源汽车的销量大幅增加,小明家新换了一辆新能源纯电汽车,他连续7天记录了每天行驶的路程(如下表),以50km为标准,多于50km的记为“$+$”,不足50km的记为“$-$”,刚好50km的记为“0”。

(1)这7天里,路程最多的一天比最少的一天多行驶49km。
(2)小明家的新能源汽车这7天一共行驶了多少千米？
$(-8)+(-12)+(-16)+0+(+22)+(+31)+(+33)=-36+86=50(km),50×7+50=400(km),$所以小明家的新能源汽车这7天一共行驶了400 km.
(3)已知新能源汽车每行驶100km耗电量为15度,每度电为0.5元,则小明家这7天的行驶费用是多少？
小明家这7天的行驶费用是$\frac {400}{100}×15×0.5=30$(元).

答案：
(1)49 根据题意,得$(+33)-(-16)=49(km),$所以这7天里路程最多的一天比最少的一天多行驶49 km.
(2)$(-8)+(-12)+(-16)+0+(+22)+(+31)+(+33)=-36+86=50(km),50×7+50=400(km),$所以小明家的新能源汽车这7天一共行驶了400 km.
(3)小明家这7天的行驶费用是$\frac {400}{100}×15×0.5=30$(元).

[回顾与思考]有理数有哪些运算律？结合例子说明运算律在有理数运算中的作用。

答案： 见解析