第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
9 根据如图所示的程序计算,若输入的x值为7,则输出的y值为

-1
.
答案:
-1 当x=7时,7+(-5)+(-3)+4=7+4+[(-5)+(-3)]=11+(-8)=3>0,继续输入,当x=3时,3+(-5)+(-3)+4=3+4+[(-5)+(-3)]=7+(-8)=-1<0,输出,故输出的y值为-1.
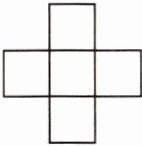
10 新情境 新趋势·结论开放 [2024陕西中考A卷]小华探究“幻方”时,提出了一个问题:如图,将0,-2,-1,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是______.(写出一个符合题意的数即可)

答案:
0(答案不唯一) 如图,根据题意,可填写如下.

0(答案不唯一) 如图,根据题意,可填写如下.

11 已知有理数$-\frac{5}{2},0,2,-|4|,-|1|,-(-1.5)$.
(1)在如图所示的数轴上标出上述有理数;
(2)用“>”号把上述有理数连接起来;
(3)求上述有理数的和.
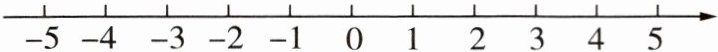
(1)在如图所示的数轴上标出上述有理数;
(2)用“>”号把上述有理数连接起来;
(3)求上述有理数的和.
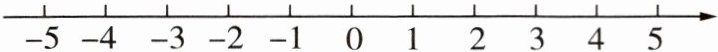
答案:
解:
(1)-|4|=-4,-|1|=-1,-(-1.5)=1.5,在数轴上表示如下.

(2)根据数轴可得,2>-(-1.5)>0>-|1|$>-\frac{5}{2}>-$|4|.
$(3)(-\frac{5}{2})+0+2+(-$|4|)+(-|1|$)+[-(-1.5)]=(-\frac{5}{2})+0+2+(-4)+(-1)+1.5=(-\frac{5}{2})+\frac{3}{2}+2+(-4)+(-1)=[(-\frac{5}{2})+\frac{3}{2}]+[2+(-4)+(-1)]=[-(\frac{5}{2}-\frac{3}{2})]+[-(4+1-2)]=-1+(-3)=-(1+3)=-4.$
解:
(1)-|4|=-4,-|1|=-1,-(-1.5)=1.5,在数轴上表示如下.

(2)根据数轴可得,2>-(-1.5)>0>-|1|$>-\frac{5}{2}>-$|4|.
$(3)(-\frac{5}{2})+0+2+(-$|4|)+(-|1|$)+[-(-1.5)]=(-\frac{5}{2})+0+2+(-4)+(-1)+1.5=(-\frac{5}{2})+\frac{3}{2}+2+(-4)+(-1)=[(-\frac{5}{2})+\frac{3}{2}]+[2+(-4)+(-1)]=[-(\frac{5}{2}-\frac{3}{2})]+[-(4+1-2)]=-1+(-3)=-(1+3)=-4.$
12 阅读下列计算方法:
$-5\frac{5}{6}+(-9\frac{2}{3})+17\frac{3}{4}+(-3\frac{1}{2})$
$=[(-5)+(-\frac{5}{6})]+[(-9)+(-\frac{2}{3})]+[(+17)+(+\frac{3}{4})]+[(-3)+(-\frac{1}{2})]$
$=[(-5)+(-9)+(+17)+(-3)]+[(-\frac{5}{6})+(-\frac{2}{3})+(+\frac{3}{4})+(-\frac{1}{2})]$
$=0+(-1\frac{1}{4})$
$=-1\frac{1}{4}$.
上面这种计算方法叫做拆项法. 仿照上述方法计算:
$(-2025\frac{5}{6})+(-2024\frac{2}{3})+4049\frac{2}{3}+(-1\frac{1}{2})$.
$-5\frac{5}{6}+(-9\frac{2}{3})+17\frac{3}{4}+(-3\frac{1}{2})$
$=[(-5)+(-\frac{5}{6})]+[(-9)+(-\frac{2}{3})]+[(+17)+(+\frac{3}{4})]+[(-3)+(-\frac{1}{2})]$
$=[(-5)+(-9)+(+17)+(-3)]+[(-\frac{5}{6})+(-\frac{2}{3})+(+\frac{3}{4})+(-\frac{1}{2})]$
$=0+(-1\frac{1}{4})$
$=-1\frac{1}{4}$.
上面这种计算方法叫做拆项法. 仿照上述方法计算:
$(-2025\frac{5}{6})+(-2024\frac{2}{3})+4049\frac{2}{3}+(-1\frac{1}{2})$.
答案:
解$:(-2025\frac{5}{6})+(-2024\frac{2}{3})+4049\frac{2}{3}+(-1\frac{1}{2})=[(-2025)+(-\frac{5}{6})]+[(-2024)+(-\frac{2}{3})]+[(+4049)+(+\frac{2}{3})]+[(-1)+(-\frac{1}{2})]=[(-2025)+(-2024)+(+4049)+(-1)]+[(-\frac{5}{6})+(-\frac{2}{3})+(+\frac{2}{3})+(-\frac{1}{2})]($注意:对于带负号的带分数,在拆项时,拆成的整数和真分数也要带上负号$)=-1+(-\frac{4}{3})=-2\frac{1}{3}.$
13 运算能力 对于有理数a,b定义新运算“△”:$a△b= b$. 关于该运算给出下列结论:①$-5△7= -5$;②$5△7= (-9)△7$;③若$a△b= b△a$,则$a= b$;④该运算满足交换律. 其中正确的是
②③
.(填序号)
答案:
②③ 因为a△b=b,所以(-5)△7=7,故①错误.因为5△7=7,(-9)△7=7,所以5△7=(-9)△7,故②正确.因为a△b=b,b△a=a,所以当a△b=b△a时,a=b,故③正确.只有当a=b时,a△b=b△a,所以该运算不满足交换律.
14 推理能力 (1)比较大小(填“>”“<”或“=”):①$|2|+|3|$
(2)已知a,b为有理数,通过比较、分析,归纳$|a|+|b|与|a+b|$的大小关系.(填“>”“<”“≥”“≤”或“=”)
①当a,b同号时,$|a|+|b|$
②当a,b异号时,$|a|+|b|$
③当$a= 0或b= 0$时,$|a|+|b|= |a+b|$.
综上,$|a|+|b|$
追问:根据(2)中的结论,当$|x|+6= |x-6|$时,x的取值范围是
=
$|2+3|$;②$|-2|+|-3|$=
$|-2-3|$;③$|2|+|-3|$>
$|2-3|$;④$|2|+|0|$=
$|2+0|$.(2)已知a,b为有理数,通过比较、分析,归纳$|a|+|b|与|a+b|$的大小关系.(填“>”“<”“≥”“≤”或“=”)
①当a,b同号时,$|a|+|b|$
=
$|a+b|$;②当a,b异号时,$|a|+|b|$
>
$|a+b|$;③当$a= 0或b= 0$时,$|a|+|b|= |a+b|$.
综上,$|a|+|b|$
≥
$|a+b|$.追问:根据(2)中的结论,当$|x|+6= |x-6|$时,x的取值范围是
x≤0
.
答案:
解:
(1)①=;②=;③>;④=
(2)①=;②>;③≥
①当a,b同为正数时,|a+b|=|a|+|b|;当a,b同为负数时,|a+b|=-(a+b)=-a+(-b)=|a|+|b|.②当a,b异号时,设a=m,b=-n(m>0,n>0),则|a|+|b|=m+n,|a+b|=|m-n|.因为m+n为两正数相加,|m-n|为两正数差的绝对值,所以m+n>|m-n|,所以|a|+|b|>|a+b|.
追问:x≤0
已知|x|+6=|x|+|-6|=|x-6|,由
(2)①③可知,x与-6同号或x=0,所以x≤0.
(1)①=;②=;③>;④=
(2)①=;②>;③≥
①当a,b同为正数时,|a+b|=|a|+|b|;当a,b同为负数时,|a+b|=-(a+b)=-a+(-b)=|a|+|b|.②当a,b异号时,设a=m,b=-n(m>0,n>0),则|a|+|b|=m+n,|a+b|=|m-n|.因为m+n为两正数相加,|m-n|为两正数差的绝对值,所以m+n>|m-n|,所以|a|+|b|>|a+b|.
追问:x≤0
已知|x|+6=|x|+|-6|=|x-6|,由
(2)①③可知,x与-6同号或x=0,所以x≤0.
查看更多完整答案,请扫码查看


