《2025年一遍过七年级数学上册华师大版》

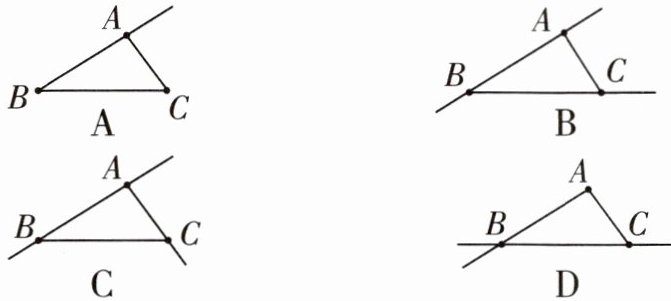
9 如图,平面内有三个点 $ A $,$ B $,$ C $,画射线 $ AB $,画直线 $ BC $,连接 $ AC $,正确的是(D)
]

答案： D

10 (1) 平面内有 $ 4 $ 个点,其中任意 $ 3 $ 个点都不在同一条直线上,经过每两点画一条直线,共可画6条；
(2) 平面内有 $ A $,$ B $,$ C $ 三点,经过任意两点画一条直线,共可画3或1条。

答案：
(1)6;
(2)3或1
(1)因为每个点都可同其他三点画一条直线,所以共可画4×3=12(条)直线.因为直线AB与直线BA是同一条直线,所以实际为12÷2=6(条)直线.
(2)若3个点不在同一条直线上,则可画出3条直线;若3个点在同一条直线上,则可画出1条直线.

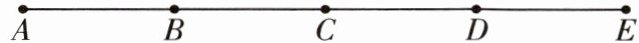
11 [2025郑州三中期末]如图,$ AE $ 是一段高铁行驶路线图,图中字母表示的 $ 5 $ 个点代表 $ 5 $ 个车站.在这段路线上往返行车,需印制20种车票。
]

答案： 20 题图中共有10条线段,分别是线段AB,线段AC,线段AD,线段AE,线段BC,线段BD,线段BE,线段CD,线段CE,线段DE,单程要10种车票,往返就是20种(线段AB和线段BA表示两种车票).

12 [2025南阳期末]如图,已知直线 $ l $ 和点 $ A $,$ B $,$ P $。

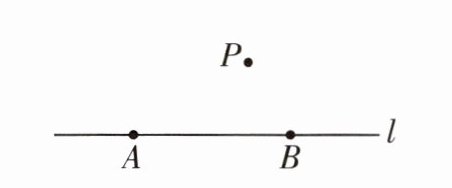
(1) 用适当的语句表述点 $ A $ 与直线 $ l $ 的位置关系：______。
(2) 按下列要求画图.(不写作法,保留作图痕迹)
①画直线 $ PA $；②画射线 $ BP $。
(3) $ BP $____$ AP + AB $(填“$ ＞ $”“$ ＜ $”或“$ = $”),理由是______。

答案：
解:
(1)点A在直线l上
(2)如图,直线PA和射线BP即所求.

(3)＜ 两点之间线段最短

13 如图,在同一平面内有 $ A $,$ B $,$ C $,$ D $ 四个点,则是否存在一点 $ P $,使 $ PA + PB + PC + PD $ 的值最小？若存在,请在图中画出点 $ P $ 的位置,并简要说明理由；若不存在,直接回答不存在即可。
]

答案：
解:存在.画图如下:
连接BD,AC,则BD与AC的交点即为点P的位置.

理由:两点之间线段最短.

14 应用意识 如图,线段 $ AB $ 上的点数与线段的总数有如下关系：若线段 $ AB $ 上有 $ 3 $ 个点,则线段的总数为 $ 3 $；若线段 $ AB $ 上有 $ 4 $ 个点,则线段的总数为 $ 6 $；若线段 $ AB $ 上有 $ 5 $ 个点,则线段的总数为 $ 10 … … $

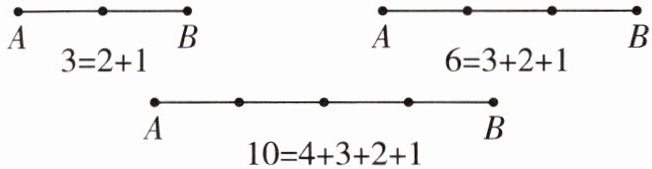
【观察思考】
(1) 若线段 $ AB $ 上有 $ 6 $ 个点,则线段的总数为15。
(2) 若线段 $ AB $ 上有 $ n $ 个点,则线段的总数是多少？(用含 $ n $ 的式子表示)
【拓展应用】
(3) 若有 $ 8 $ 位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),根据上述模型,本次一共要进行多少场比赛？
追问：若第(3)问的比赛采用双循环制(即每两位同学之间都要进行两场比赛),则本次一共要进行56场。

答案： 解:
(1)15 15=1+2+3+4+5.
(2)若线段AB上有n个点,则线段的总数为1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$.
(3)把8位同学看成直线上的8个点,每两位同学之间的一场比赛看成一条线段(抽象思想).
根据
(2)中的结论可得,当n=8时,$\frac{n(n-1)}{2}=\frac{8×7}{2}=28$.
答:一共要进行28场比赛.
追问:56
根据
(3)可得,当单循环比赛时,共赛28场,则双循环比赛时,需赛28×2=56(场).
名师点睛
本题第
(2)问,1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$可根据下面计算过程得到:
1 + 2 + 3 +…+(n-3)+(n-2)+(n-1)
(n-1)+(n-2)+(n-3)+…+ 3 + 2 + 1
↓
上下两行数对应相加得n,每行是(n-1)个数,即(n-1)个n相加,为n(n-1).因为是两行,所以需要除以2,所以1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$.