《2025年一遍过七年级数学上册华师大版》

1 对式子$(-\frac{3}{5}+\frac{1}{2})×(-4)×(-25)$进行简便计算,如图所示,则运用到的运算律①是(C)
$\begin{aligned}&(-\frac{3}{5}+\frac{1}{2})×(-4)×(-25)\\=&(-\frac{3}{5}+\frac{1}{2})×[(-4)×(-25)]…(①)\\=&(-\frac{3}{5}+\frac{1}{2})×100\\=&(-\frac{3}{5})×100+\frac{1}{2}×100\\=&-60+50= -10.\end{aligned} $
A.乘法交换律
B.分配律
C.乘法结合律
D.加法交换律

答案： C

2 计算：
(1)$-\frac{1}{5}×2^{2}+\frac{1}{5}×6^{2}$；
(2)$(\frac{1}{3}-\frac{1}{5})×(-15)÷|-\frac{1}{3}|+1^{2}-2×(-0.125)×8$。

答案： 解:
(1)$-\frac {1}{5}×2^{2}+\frac {1}{5}×6^{2}=\frac {1}{5}×(-2^{2}+6^{2})=\frac {1}{5}×(-4+36)=\frac {32}{5}.$
(2)$(\frac {1}{3}-\frac {1}{5})×(-15)÷|-\frac {1}{3}|+1^{2}-2×(-0.125)×8=(\frac {1}{5}×15-\frac {1}{3}×15)÷\frac {1}{3}+1-2×(-0.125×8)=(-2)×3+1-(-2)=-6+1+2=-3.$

3 教材P61例4变式 计算$(\frac{1}{2}-\frac{2}{3}-\frac{3}{4})×12$,下面是甲、乙两位同学的部分运算过程：

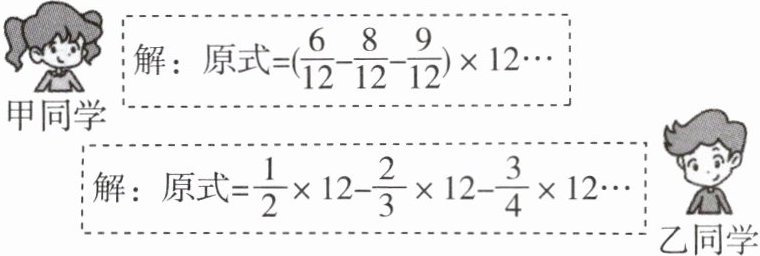
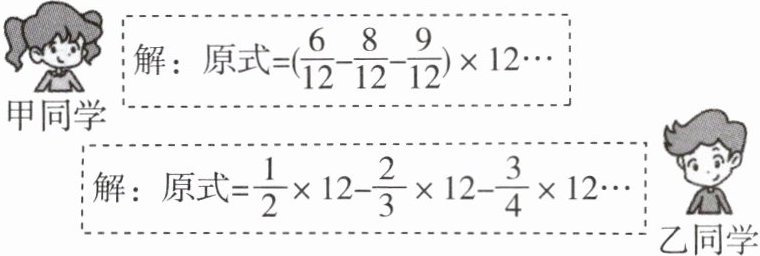
(1)甲同学的依据是①,乙同学的依据是②；(填序号)
①分数的基本性质；②分配律；
③乘法交换律
(2)请选择一种你认为简便的解法,写出完整的计算过程。
选乙同学:$(\frac {1}{2}-\frac {2}{3}-\frac {3}{4})×12=\frac {1}{2}×12-\frac {2}{3}×12-\frac {3}{4}×12=6-8-9=-11.$

答案：
(1)① ②；
(2)选甲同学:$(\frac {1}{2}-\frac {2}{3}-\frac {3}{4})×12=(\frac {6}{12}-\frac {8}{12}-\frac {9}{12})×12=-\frac {11}{12}×12=-11.$选乙同学:$(\frac {1}{2}-\frac {2}{3}-\frac {3}{4})×12=\frac {1}{2}×12-\frac {2}{3}×12-\frac {3}{4}×12=6-8-9=-11.$

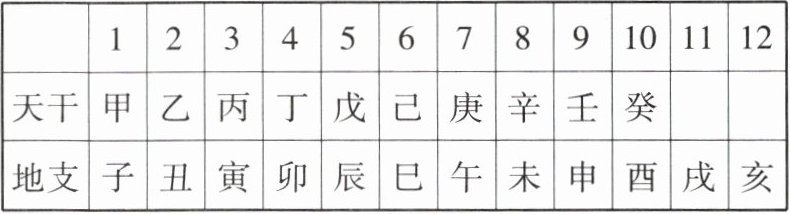
4 [2025重庆北碚区期末]干支纪年法是中国历法上一直使用的纪年方法,干支是天干和地支的总称。“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”十个符号叫天干；“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”十二个符号叫地支。把干支按顺序相配(甲子、乙丑、丙寅……),正好六十为一周期,周而复始,循环记录,这就是俗称的“干支表”(如下),如2025年为乙巳年。根据上述规律,可得2050年为(C)

A.癸亥年
B.己丑年
C.庚午年
D.甲子年

答案： C 2050-2025=25(年),25÷10=2……5,所以2050年的天干为从“乙”往后数5个,即为庚,25÷12=2……1,所以2050年的地支为从“巳”往后数1个,即为午,所以2050年为庚午年.

5 某公司去年前3个月平均每月盈利$-1.5$万元,4~6月平均每月盈利2万元,7~10月平均每月盈利1.2万元,最后两个月平均每月盈利$-3.3$万元,则这个公司去年总盈利是-0.3万元。

答案： -0.3 由题意,可知这个公司去年总盈利是$-1.5×3+2×3+1.2×4-3.3×2=-4.5+6+4.8-6.6=-0.3$(万元).