第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
1 有理数 $ a,b $ 在数轴上的对应点的位置如图所示,下列结论正确的是 (
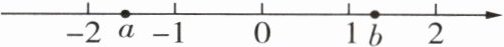
A.$ a < -2 $
B.$ b < 1 $
C.$ a > b $
D.$ a < b $
D
)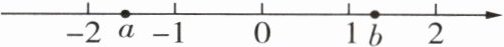
A.$ a < -2 $
B.$ b < 1 $
C.$ a > b $
D.$ a < b $
答案:
D 根据题中数轴,可知a > -2,b > 1,a < b.
变式如图,数轴上的点分别表示有理数 $ a,b $.若 $ a > b $,则其中表示正确的图形是 (
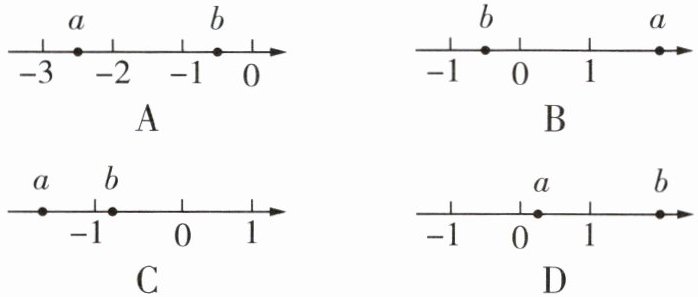
B
)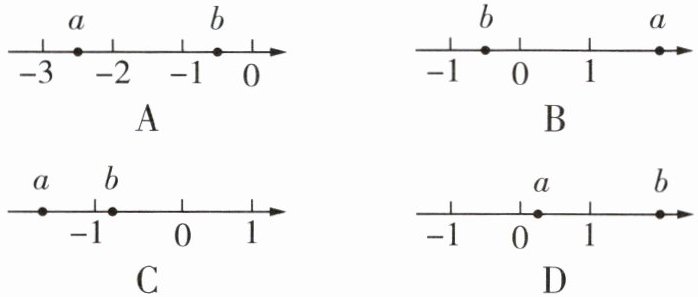
答案:
B 根据a > b,知道在数轴上数a对应的点在b对应点的右边,故选 B.
2 在数轴上,因为表示 $ -6 $ 的点在原点的
左
边,所以 $ 0 $>
$ -6 $;因为表示 $ -4.5 $ 的点在表示 $ -2\frac{1}{3} $ 的点的左
边,所以 $ -4.5 $<
$ -2\frac{1}{3} $.(填“左”“右”“>”或“<”)
答案:
左 > 左 <
3 如图,在数轴上有 $ A,B,C $ 三个点.
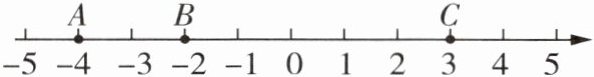
(1)将点 $ B $ 向左移动 $ 4 $ 个单位长度后,点
(2)将点 $ A $ 向右移动 $ 3 $ 个单位长度后,点
(3)将点 $ C $ 向左移动 $ 6 $ 个单位长度后,点 $ B $ 所表示的数比点 $ C $ 所表示的数大
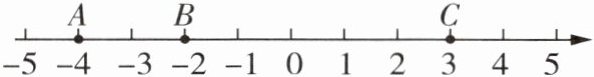
(1)将点 $ B $ 向左移动 $ 4 $ 个单位长度后,点
B
所表示的数最小,是-6
;(2)将点 $ A $ 向右移动 $ 3 $ 个单位长度后,点
B
所表示的数最小,是-2
;(3)将点 $ C $ 向左移动 $ 6 $ 个单位长度后,点 $ B $ 所表示的数比点 $ C $ 所表示的数大
1
.
答案:
(1)B -6;
(2)B -2;
(3)1
(1)B -6;
(2)B -2;
(3)1
4 [2025嘉兴期中]如图,数轴上每个刻度为 $ 1 $ 个单位长度,点 $ A $ 表示的数是 $ -3 $.
(1)在数轴上标出原点,则点 $ B $ 所表示的数是多少?
(2)在数轴上找出点 $ C $,使它与点 $ B $ 的距离为 $ 2 $ 个单位长度,则点 $ C $ 表示的数为______.
(3)在数轴上表示下列各数,并用“<”号把这些数连接起来.
$ 2.5,-4,5\frac{1}{2},-2\frac{1}{2},1.5,-1.6 $.

(1)在数轴上标出原点,则点 $ B $ 所表示的数是多少?
(2)在数轴上找出点 $ C $,使它与点 $ B $ 的距离为 $ 2 $ 个单位长度,则点 $ C $ 表示的数为______.
(3)在数轴上表示下列各数,并用“<”号把这些数连接起来.
$ 2.5,-4,5\frac{1}{2},-2\frac{1}{2},1.5,-1.6 $.

答案:
解:
(1)原点如图1所示.

点 B 所表示的数是4.
(2)2或6
当点 C 在点 B 的左边时,点 C 表示的数是2;当点 C 在点 B 的右边时,点 C 表示的数是6.
(3)在数轴上表示各数如图2所示.

由数轴可知,$-4 < -2\frac{1}{2} < -1.6 < 1.5 < 2.5 < 5\frac{1}{2}$.
解:
(1)原点如图1所示.

点 B 所表示的数是4.
(2)2或6
当点 C 在点 B 的左边时,点 C 表示的数是2;当点 C 在点 B 的右边时,点 C 表示的数是6.
(3)在数轴上表示各数如图2所示.

由数轴可知,$-4 < -2\frac{1}{2} < -1.6 < 1.5 < 2.5 < 5\frac{1}{2}$.
5 画出数轴,并解决下列问题.
(1)把 $ 4,-3.5,\frac{1}{2},-1\frac{1}{2},0,2.5 $ 表示在数轴上;
(2)请将上面的数用“<”号连接起来;
(3)观察数轴,写出大于 $ -4\frac{1}{3} $ 的所有负整数.
(1)把 $ 4,-3.5,\frac{1}{2},-1\frac{1}{2},0,2.5 $ 表示在数轴上;
(2)请将上面的数用“<”号连接起来;
(3)观察数轴,写出大于 $ -4\frac{1}{3} $ 的所有负整数.
答案:
解:
(1)如图所示.

(2)由
(1)得$-3.5 < -1\frac{1}{2} < 0 < \frac{1}{2} < 2.5 < 4$.
(3)由
(1)中数轴得大于$-4\frac{1}{3}$的所有负整数有-4,-3,-2,-1.
解:
(1)如图所示.

(2)由
(1)得$-3.5 < -1\frac{1}{2} < 0 < \frac{1}{2} < 2.5 < 4$.
(3)由
(1)中数轴得大于$-4\frac{1}{3}$的所有负整数有-4,-3,-2,-1.
6 [2024贵州中考]下列有理数中最小的数是 (
A.$ -2 $
B.$ 0 $
C.$ 2 $
D.$ 4 $
A
)A.$ -2 $
B.$ 0 $
C.$ 2 $
D.$ 4 $
答案:
A 因为-2 < 0 < 2 < 4,所以最小的数是-2.
7 [新趋势·结论开放][2024湖北中考]写出一个大于 $ -1 $ 的数:
0(答案不唯一)
.
答案:
0(答案不唯一)
8 甲地海拔为 $ 30 m $,乙地海拔为 $ 20 m $,丙地海拔为 $ -5 m $.甲、乙、丙三地中最高处为
甲
地,最低处为丙
地.
答案:
甲 丙 易知三个数中30最大,-5最小,故最高处为甲地,最低处为丙地.
9 [教材P13习题T8变式]给出下列说法:① $ 0 $ 是最小的有理数;②若有理数 $ m > n $,则数轴上表示 $ m $ 的点一定在表示 $ n $ 的点的左边;③在数轴上表示有理数的点离原点越远,这个有理数就越大;④ $ 0 $ 是最小的非负整数,也是最大的非正整数.其中正确的是
④
.(填序号)
答案:
④ 不存在最小的有理数,①错误;若有理数m > n,则数轴上表示m的点一定在表示n的点的右边,②错误;在数轴上,表示-5的点比表示1的点离原点远,但-5 < 1,所以③错误.
查看更多完整答案,请扫码查看


