《2025年一遍过七年级数学上册华师大版》

13 如图,直线AB与CD被直线EF所截,分别交AB,CD于点F,M,过点M作射线MN,则图中与∠1是同位角的是(B)

A.∠3
B.∠2或∠DME
C.∠2或∠3
D.∠2或∠3或∠DME

答案： B

14 [2025上海段考]若两个角是内错角,则这两个角不一定相等。(填“一定不”“不一定”或“一定”)

答案： 不一定

15 [2025上海徐汇区期末]如图,若∠2 = 100°,则∠1的同位角的度数为______。

答案：
80° 如图,因为∠1的同位角是∠3,且∠2+∠3=180°,所以∠3=180°−∠2=180°−100°=80°.

16 如图,能与∠B构成同旁内角的角有3个。

答案： 3 由题图,可知能与∠B构成同旁内角的角有∠BAC,∠C,∠BAE,共3个.

变式 图中同旁内角共有5对。

答案： 5 ∠OQP与∠OPQ是同旁内角,∠DQP与∠BPQ是同旁内角，∠QOP与∠OQP是同旁内角，∠EQO与∠AOQ是同旁内角，∠QOP与∠QPO是同旁内角，所以共有5对

17 教材P178试一试变式 如图,在三角形ABC所在的平面内画一条直线,使得与∠A是同旁内角的角有3个(画在图1中)或4个(画在图2中),并在图上标出这些角。

答案：
解:如图1,与∠A是同旁内角的角有3个,分别是∠1,∠B,∠C.
如图2,与∠A是同旁内角的角有4个,分别是∠2,∠3,∠B,∠C.

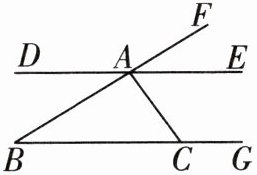
18 如图,BF,DE相交于点A,BG,BF交于点B,BG,AC交于点C。
(1)写出DE,BC被BF所截形成的同位角,内错角,同旁内角；
(2)写出DE,BC被AC所截形成的内错角；
(3)写出FB,BC被AC所截形成的同旁内角。

答案：
(1)同位角为∠FAE与∠B,内错角为∠B与∠DAB,同旁内角为∠EAB与∠B.
(2)内错角为∠EAC与∠BCA,∠DAC与∠ACG.
(3)同旁内角为∠BAC与∠BCA,∠FAC与∠ACG.

19 两条直线被第三条直线所截,∠1与∠2是同旁内角,∠3与∠2是内错角。
(1)画出示意图；
(2)若∠1 = 3∠2,∠2 = 3∠3,求∠1,∠2的度数。

答案：

(1)如图.(答案不唯一)

(2)因为∠1=3∠2,∠2=3∠3,所以∠1=9∠3.
又因为∠1+∠3=180°,
所以∠1=$\frac{9}{9+1}$×180°=162°,所以∠2=$\frac{1}{3}$∠1=54°.

20 推理能力(1)如图1,直线$l_1,l_2$被直线$l_3$所截,图中共有4对同位角,2对内错角,2对同旁内角。
(2)如图2,直线$l_1,l_2,l_3$两两相交,图中共有12对同位角,6对内错角,6对同旁内角。
(3)如图3,直线$l_1,l_2$与直线$l_3,l_4$相交,图中共有32对同位角,16对内错角,16对同旁内角。

答案：
(1)4 2 2;
(2)12 6 6;
(3)32 16 16

[回顾与思考]下面是本节学到的一些数学名词：邻补角、对顶角、垂直、同位角、内错角、同旁内角,你能用自己的语言描述它们吗？你能分别画一个图形表示它们吗？

答案： （图形略，按上述描述绘制即可）