第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
已知平面上的三个点 $ A,B,C $.
【基础设问】
(1)如图,点 $ A,B,C $ 不在同一条直线上,请根据下列要求画图:
①画直线 $ AC $;②画射线 $ BA $;③画线段 $ BC $.
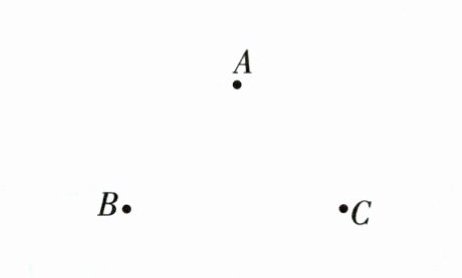
(2)在(1)的条件下,图中共有______条射线,$ \angle BAC $ 的补角是______.
(3)图中从点 $ B $ 到点 $ C $ 的最短路径是______,依据是______.
(4)①请你用量角器或三角板在(1)中画 $ \angle ABC $的余角、角平分线及 $ \angle ACB $ 的平分线,$ \angle ABC $的平分线与 $ \angle ACB $ 的平分线交于点 $ H $.
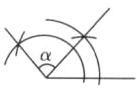
②已知(1)中 $ \angle ABC $ 和 $ \angle BCA $ 的补角 $ \angle BCF $,利用尺规作图作 $ \angle \alpha $,使 $ \angle \alpha=\angle BCF-\angle ABC $.(不写作法,保留作图痕迹)
③在①的条件下,若 $ \angle BAC = 50^{\circ} $,求 $ \angle BHC $的度数.
【能力设问】
(5)如图,点 $ C $ 在线段 $ AB $ 上,$ M,N $ 分别为 $ AC $,$ AB $ 的中点.
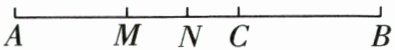
①若 $ AC = 12\mathrm{cm},BC = 8\mathrm{cm} $,求 $ MN $ 的长.
②若 $ BC = 10\mathrm{cm} $,求 $ MN $ 的长.
(6)小明在彩纸上画了一条长为 $ 20\mathrm{cm} $ 的线段 $ AB $,将其四等分后画了五个小正方形(如图).
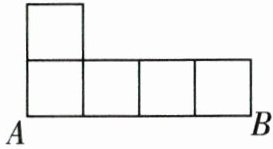
①若该平面图形是某几何体的俯视图,将这五个小正方形中填上数(如图),请你在下面的方格中画出该几何体的主视图和左视图.
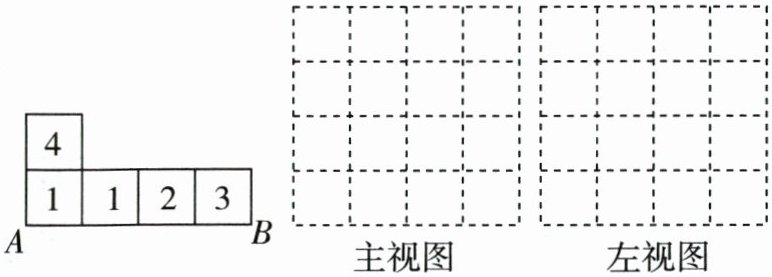
②如图,若该平面图形是某无盖正方体的展开图,则折叠后与点 $ A,R,K,Q $ 分别重合的点是哪些?
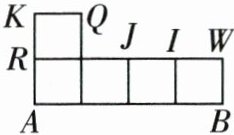
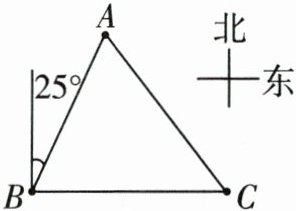
(7)如图,若(1)中的 $ B,C $ 处是码头,$ A $ 处是灯塔,在码头 $ B $ 处测得海中灯塔 $ A $ 在北偏东 $ 25^{\circ} $方向上. 若 $ \angle ACB= \frac{4}{5}\angle ABC $,则灯塔 $ A $ 在码头 $ C $ 的什么方向上?
【基础设问】
(1)如图,点 $ A,B,C $ 不在同一条直线上,请根据下列要求画图:
①画直线 $ AC $;②画射线 $ BA $;③画线段 $ BC $.
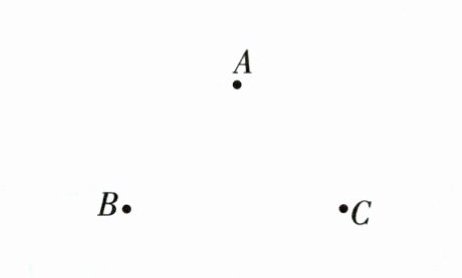
(2)在(1)的条件下,图中共有______条射线,$ \angle BAC $ 的补角是______.
(3)图中从点 $ B $ 到点 $ C $ 的最短路径是______,依据是______.
(4)①请你用量角器或三角板在(1)中画 $ \angle ABC $的余角、角平分线及 $ \angle ACB $ 的平分线,$ \angle ABC $的平分线与 $ \angle ACB $ 的平分线交于点 $ H $.
②已知(1)中 $ \angle ABC $ 和 $ \angle BCA $ 的补角 $ \angle BCF $,利用尺规作图作 $ \angle \alpha $,使 $ \angle \alpha=\angle BCF-\angle ABC $.(不写作法,保留作图痕迹)
③在①的条件下,若 $ \angle BAC = 50^{\circ} $,求 $ \angle BHC $的度数.
【能力设问】
(5)如图,点 $ C $ 在线段 $ AB $ 上,$ M,N $ 分别为 $ AC $,$ AB $ 的中点.
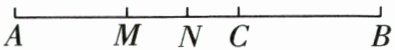
①若 $ AC = 12\mathrm{cm},BC = 8\mathrm{cm} $,求 $ MN $ 的长.
②若 $ BC = 10\mathrm{cm} $,求 $ MN $ 的长.
(6)小明在彩纸上画了一条长为 $ 20\mathrm{cm} $ 的线段 $ AB $,将其四等分后画了五个小正方形(如图).

①若该平面图形是某几何体的俯视图,将这五个小正方形中填上数(如图),请你在下面的方格中画出该几何体的主视图和左视图.

②如图,若该平面图形是某无盖正方体的展开图,则折叠后与点 $ A,R,K,Q $ 分别重合的点是哪些?
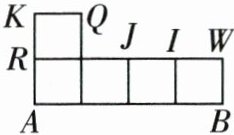
(7)如图,若(1)中的 $ B,C $ 处是码头,$ A $ 处是灯塔,在码头 $ B $ 处测得海中灯塔 $ A $ 在北偏东 $ 25^{\circ} $方向上. 若 $ \angle ACB= \frac{4}{5}\angle ABC $,则灯塔 $ A $ 在码头 $ C $ 的什么方向上?

答案:
(1)①如图,直线AC即所求.②射线BA即所求.③线段BC即所求.
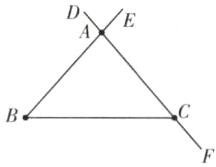
(2)6 ∠BAD和∠CAE
图中的射线分别为射线BA,射线CA,射线CF,射线AC,射线AD,射线AE,共6条.
(3)线段BC 两点之间线段最短
(4)①如图,∠ABG是∠ABC的余角,BH和CH分别是∠ABC和∠ACB的平分线.
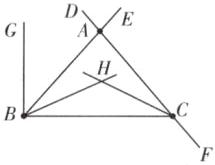
②如图,∠α即所求.
③因为∠BAC=50°,
所以∠ABC+∠ACB=180° - 50°=130°,
所以∠HBC+∠HCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,所以∠BHC=180°-(∠HBC+∠HCB)=180° - 65°=115°.
(5)①因为AC=12 cm,BC=8 cm,
所以AB=AC+BC=12+8=20(cm).
因为M,N分别为AC,AB的中点,
所以AM=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6(cm),AN=$\frac{1}{2}$AB=$\frac{1}{2}$×20=10(cm),
所以MN=AN - AM=10 - 6=4(cm).
②因为M,N分别为AC,AB的中点,
所以AM=$\frac{1}{2}$AC,AN=$\frac{1}{2}$AB,
所以MN=AN - AM=$\frac{1}{2}$(AB - AC)=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5(cm).
(6)①该几何体的主视图和左视图如图所示.
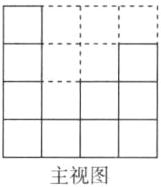
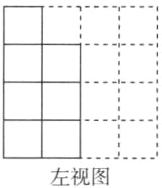
②与点A重合的是点B,与点R重合的是点W,与点K重合的是点I,与点Q重合的是点J.
(7)根据题意,得∠ABC=90° - 25°=65°.
因为∠ACB=$\frac{4}{5}$∠ABC,所以∠ACB=$\frac{4}{5}$×65°=52°.
因为90° - 52°=38°,
所以灯塔A在码头C的北偏西38°方向上.
(1)①如图,直线AC即所求.②射线BA即所求.③线段BC即所求.

(2)6 ∠BAD和∠CAE
图中的射线分别为射线BA,射线CA,射线CF,射线AC,射线AD,射线AE,共6条.
(3)线段BC 两点之间线段最短
(4)①如图,∠ABG是∠ABC的余角,BH和CH分别是∠ABC和∠ACB的平分线.

②如图,∠α即所求.

③因为∠BAC=50°,
所以∠ABC+∠ACB=180° - 50°=130°,
所以∠HBC+∠HCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,所以∠BHC=180°-(∠HBC+∠HCB)=180° - 65°=115°.
(5)①因为AC=12 cm,BC=8 cm,
所以AB=AC+BC=12+8=20(cm).
因为M,N分别为AC,AB的中点,
所以AM=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6(cm),AN=$\frac{1}{2}$AB=$\frac{1}{2}$×20=10(cm),
所以MN=AN - AM=10 - 6=4(cm).
②因为M,N分别为AC,AB的中点,
所以AM=$\frac{1}{2}$AC,AN=$\frac{1}{2}$AB,
所以MN=AN - AM=$\frac{1}{2}$(AB - AC)=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5(cm).
(6)①该几何体的主视图和左视图如图所示.


②与点A重合的是点B,与点R重合的是点W,与点K重合的是点I,与点Q重合的是点J.
(7)根据题意,得∠ABC=90° - 25°=65°.
因为∠ACB=$\frac{4}{5}$∠ABC,所以∠ACB=$\frac{4}{5}$×65°=52°.
因为90° - 52°=38°,
所以灯塔A在码头C的北偏西38°方向上.
查看更多完整答案,请扫码查看


