《2025年一遍过七年级数学上册华师大版》

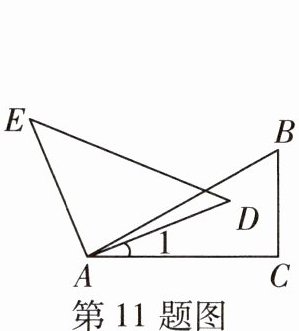
11 [2025 抚顺期末]如图,将一个三角板 30°角的顶点与另一个三角板的直角顶点重合.若∠1 = 22°25',则∠BAE 的度数为(D)

A.7°35'
B.22°25'
C.67°35'
D.82°25'

答案： D 根据题意,得∠DAE=90°,∠BAC=30°.因为∠1=22°25',所以∠BAD=∠BAC-∠1,所以∠BAE=∠DAE-∠BAD=90°-(∠BAC-∠1)=90°-30°+∠1=82°25'.

12 如图,若∠AOB = $\frac{1}{3}$∠BOC,∠COD = ∠AOD = 4∠AOB,则∠COD 的度数是120°.

答案： 120° 因为1周角=360°,所以∠COD+∠AOD+∠AOB+∠BOC=360°.因为∠COD=∠AOD=4∠AOB,∠BOC=3∠AOB,所以4∠AOB+4∠AOB+∠AOB+3∠AOB=360°,所以∠AOB=30°,所以∠COD=4×30°=120°.

13 [2025 深圳宝安中学开学考试]如图,在长方形纸片 ABCD 中,M 为 AD 边上的一点,将纸片沿 BM,CM 折叠,使点 A 落在点$ A_1 $处,点 D 落在点$ D_1 $处.若∠1 = 30°,则∠BMC 的度数为______.

105°

答案： 105° 根据折叠的性质,得∠AMB=∠A₁MB= $\frac{1}{2}$∠AMA₁,∠DMC=∠D₁MC= $\frac{1}{2}$∠DMD₁.因为∠1=30°,所以∠AMB+∠DMC= $\frac{1}{2}$∠AMA₁+ $\frac{1}{2}$∠DMD₁= $\frac{1}{2}$(∠AMA₁+∠DMD₁)= $\frac{1}{2}$(180°-∠1)= $\frac{1}{2}$×(180°-30°)=75°,所以∠BMC=180°-(∠AMB+∠DMC)=180°-75°=105°.

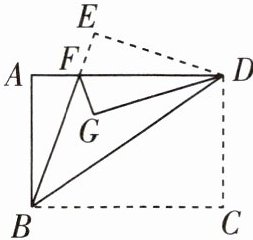
变式 [2025 毕节期末]如图,将一张长方形纸片 ABCD 沿 BD 折叠,点 C 落在点 E 处,BE 与 AD 交于点 F,将△DEF 沿 DF 折叠,点 E 落在点 G 处.若 DG 平分∠ADB,求∠ADB 的度数.

答案： 变式 解:根据折叠的性质,得∠BDC=∠BDE,∠EDF=∠GDF.因为DG平分∠ADB,所以∠BDG=∠GDF,所以∠EDF=∠BDG=∠GDF,所以∠BDE=∠EDF+∠GDF+∠BDG=3∠GDF,所以∠BDC=∠BDE=3∠GDF,∠BDA=∠GDF+∠BDG=2∠GDF.因为∠BDC+∠BDA=90°=3∠GDF+2∠GDF=5∠GDF,所以∠GDF=18°,所以∠ADB=2∠GDF=2×18°=36°.

14 教材 P161 练习 T4 变式 如图,已知∠α 和∠β,利用尺规作∠AOB = 2∠α + ∠β.(不写作法,保留作图痕迹)

答案：
解:如图2所示.

15 推理能力 [2025 南昌期末]探究三角板中的数学.
【观察分析】
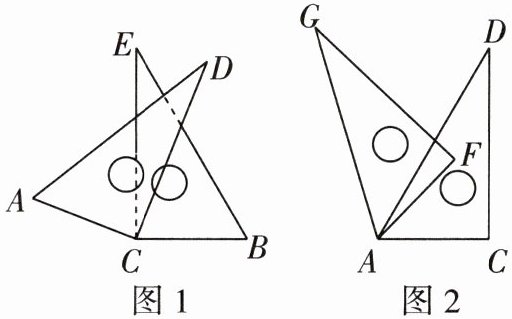
(1)如图 1,将两个同样的直角三角板的直角顶点 C 叠放在一起,∠ACD = ∠ECB = 90°.
①若∠ECD = 35°,则∠ACB = 145°；
②若∠ACB = 140°,则∠ECD = 40°；
③猜想∠ACB 与∠ECD 的数量关系为∠ACB+∠ECD=180°.
【拓展应用】
(2)如图 2,将两个同样的直角三角板的 60°锐角的顶点重合在一起,∠DAC = ∠GAF = 60°,求∠GAC + ∠DAF 的度数.

因为∠GAC=∠GAD+∠DAF+∠FAC，所以∠GAC+∠DAF=∠GAD+∠DAF+∠FAC+∠DAF=∠GAF+∠DAC。因为∠DAC=∠GAF=60°，所以∠GAC+∠DAF=60°+60°=120°。

答案： 解:
(1)①145°;②40°;③∠ACB+∠ECD=180°
①因为∠ACD=∠BCE=90°,∠ECD=35°,所以∠ACB=∠ACD+∠BCE-∠ECD=90°+90°-35°=145°.②因为∠ACD=∠BCE=90°,∠ACB=140°,所以∠ECD=∠ACD+∠BCE-∠ACB=90°+90°-140°=40°.
(2)因为∠GAC=∠GAD+∠DAF+∠FAC,所以∠GAC+∠DAF=∠GAD+∠DAF+∠FAC+∠DAF=∠GAF+∠DAC.因为∠DAC=∠GAF=60°,所以∠GAC+∠DAF=60°+60°=120°.