《2025年名师测控七年级数学上册人教版贵州专版》

1. 在某届科技大赛中,甲团队在机器人竞赛与编程竞赛项目中共获得 44 个奖项,且编程竞赛获得的奖项比机器人竞赛获得奖项的 2 倍少 4 个. 分别求编程竞赛与机器人竞赛获得奖项的个数.

答案： 解:设编程竞赛获得x个奖项,则机器人竞赛获得(44-x)个奖项.根据题意,得x+4=2(44-x).解得x=28.所以44-x=44-28=16.答:编程竞赛获得28个奖项,机器人竞赛获得16个奖项.

2. 在一次劳动课上,有 24 名同学在甲处劳动,有 18 名同学在乙处劳动,现在从乙处调一部分人去支援甲处,使得在甲处的人数比在乙处人数的 2 倍多 3 人,应从乙处调往甲处多少人？

答案： 解:设应从乙处调往甲处x人.根据题意,得24+x=2(18-x)+3.解得x=5.答:应从乙处调往甲处5人.

3. (2025·贵州一模)我国古代数学著作之一《孙子算经》中记载着这样一个问题：今有四人共车,二车空；三人共车,6 人步,问人与车各几何？意思是：今有若干人乘车,若每 4 人共乘 1 辆车,最终剩余 2 辆车；若每 3 人共乘 1 辆车,最终剩余 6 个人无车可乘,问共有多少人,多少辆车？设共有 x 辆车,根据题意所列方程正确的是(B)
A.$4(x + 2) = 3x + 6$
B.$4(x - 2) = 3x + 6$
C.$4x - 2 = 3x + 6$
D.$4x + 2 = 3x - 6$

答案： B

4. 丢番图的墓志铭.
古希腊数学家丢番图被认为是代数学的鼻祖,但历史上没有一本正式的著作里留下他完整的生平介绍,甚至连他的国籍都没有明确的记载,然而有趣的是,他竟然有一个墓志铭,上面镌刻着他的一些情况：“他生命的六分之一是幸福的童年,再活十二分之一,颊上长出了细细须. 又过了生命的七分之一才结婚. 再过 5 年,他感到很幸福,得了一个儿子. 可是这孩子光辉灿烂的生命只有他父亲的一半,儿子死后,他在悲痛中活了 4 年,结束了尘世的生涯.”你知道丢番图结婚时和去世时的年龄分别是多少吗？

答案： 解:设丢番图去世时的年龄是x岁.根据题意,得$x=\frac{1}{6}x+\frac{1}{12}x+\frac{1}{7}x+5+\frac{1}{2}x+4$.解得x=84.$84× \left( \frac{1}{6}+\frac{1}{12}+\frac{1}{7} \right)=33$(岁).答:丢番图结婚时的年龄是33岁,去世时的年龄是84岁.

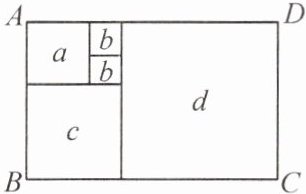
5. 如果一个长方形内部能用一些正方形铺满,既不重叠,又无缝隙,就称它为“优美长方形”. 如图,“优美长方形”ABCD 的周长为 26,则正方形 d 的边长为5.

答案： 5

6. 如图,一个酒瓶的容积为 500 mL,瓶子内还剩有一些黄酒. 当瓶子正放时,瓶内黄酒的高度为 12 cm,倒放时,空余部分的高度为 8 cm,求该瓶子的底面积$(1 mL = 1 cm^3).$

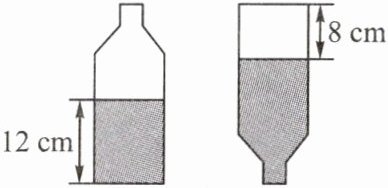
答案： 解:设瓶子的底面积为$x\ cm^2$.根据题意,得(8+12)x=500.解得x=25.答:该瓶子的底面积为$25\ cm^2$.