第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
月历中的奥秘与自然数被3整除的规律【落实课标】
活动1 月历中的奥秘
观察:2025年6月的月历如下:

探究1:(1)任意横行三个相邻数的关系:从左到右,后面的数比前面的数多____,即依次递增____;
(2)若中间的数用字母a表示,在图①上补充前后两个数:

探究2:(1)任意竖列三个相邻数的关系:从上到下,下面的数比上面的数多____,即依次递增____;
(2)若中间的数用字母a表示,在图②上补充上、下两个数.
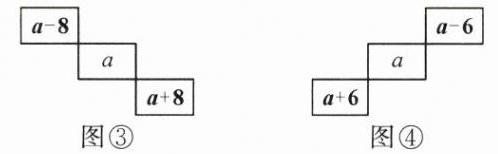
探究3:任意成对角线的三个相邻数,若中间的数用字母a表示,分别在图③、图④上补充其余两个数.

创设问题情境1:根据上述探究,利用整式的加减分别计算出四种情况下三数之和,观察结果,总结出月历中三个相邻数之间的等量关系.
(1)如图①,任意横行三个相邻数的和为______+a+______= ______;
(2)如图②,任意竖列三个相邻数的和为______+a+______= ______;
(3)如图③,任意斜下三个相邻数的和为______+a+______= ______;
(4)如图④,任意斜上三个相邻数的和为______+a+______= ______.
归纳总结:同一直线上,三个相邻数的和等于中间数的______倍.
活动1 月历中的奥秘
观察:2025年6月的月历如下:

探究1:(1)任意横行三个相邻数的关系:从左到右,后面的数比前面的数多____,即依次递增____;
(2)若中间的数用字母a表示,在图①上补充前后两个数:

探究2:(1)任意竖列三个相邻数的关系:从上到下,下面的数比上面的数多____,即依次递增____;
(2)若中间的数用字母a表示,在图②上补充上、下两个数.
探究3:任意成对角线的三个相邻数,若中间的数用字母a表示,分别在图③、图④上补充其余两个数.

创设问题情境1:根据上述探究,利用整式的加减分别计算出四种情况下三数之和,观察结果,总结出月历中三个相邻数之间的等量关系.
(1)如图①,任意横行三个相邻数的和为______+a+______= ______;
(2)如图②,任意竖列三个相邻数的和为______+a+______= ______;
(3)如图③,任意斜下三个相邻数的和为______+a+______= ______;
(4)如图④,任意斜上三个相邻数的和为______+a+______= ______.
归纳总结:同一直线上,三个相邻数的和等于中间数的______倍.
答案:
探究1:
(1)1 1
(2)解:如图①所示.
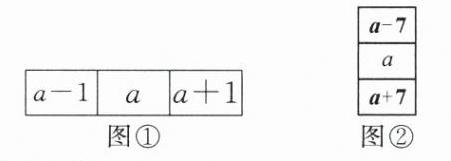
探究2:
(1)7 7
(2)解:如图②所示.
探究3:解:如图③、图④所示.
创设问题情境1:
(1)(a - 1) (a + 1) 3a
(2)(a - 7) (a + 7) 3a
(3)(a - 8) (a + 8) 3a
(4)(a - 6) (a + 6) 3a
归纳总结:3
探究1:
(1)1 1
(2)解:如图①所示.
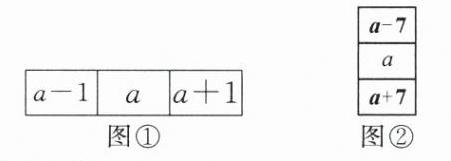
探究2:
(1)7 7
(2)解:如图②所示.
探究3:解:如图③、图④所示.

创设问题情境1:
(1)(a - 1) (a + 1) 3a
(2)(a - 7) (a + 7) 3a
(3)(a - 8) (a + 8) 3a
(4)(a - 6) (a + 6) 3a
归纳总结:3
学以致用1:某月的月历上,一个竖列上相邻三个数之和不可能是(
A.30
B.36
C.40
D.42
C
)A.30
B.36
C.40
D.42
答案:
C
【变式题】小秦在6月份的月历上圈出了三个数,其中最大的数为n,并求出它们的和为60,则这三个数在月历中的位置不可能是(

B
)
答案:
B
创设问题情境2:如图,用“2×2”(行×列)的方框在月历上任意框出四个数,若用字母a表示最小的数,分别用含a的式子表示出图上另外三个数.这四个数之间有什么等量关系?先观察,猜想再验证.


答案:

解:填数如图所示.通过观察易得斜对角两数之和相等.验证如下:因为a+(a+8)=2a+8,(a+1)+(a+7)=2a+8,所以a+(a+8)=(a+1)+(a+7).(答案不唯一,如:纵列两数之差相等,言之有理即可)

解:填数如图所示.通过观察易得斜对角两数之和相等.验证如下:因为a+(a+8)=2a+8,(a+1)+(a+7)=2a+8,所以a+(a+8)=(a+1)+(a+7).(答案不唯一,如:纵列两数之差相等,言之有理即可)
查看更多完整答案,请扫码查看


