第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
活动2 填幻方
(教材P58活动2变式)相传大禹在治洛水的时候,洛水神龟献给大禹一本洛书,书中有一幅奇怪的图(如图①所示),这幅图用今天的符号翻译出来,就是一个三阶幻方,也就是在3×3的方阵中填入9个数,每行、每列和每条对角线上的数字和相等.如图②,这是一个三阶幻方的一部分,则图中“?”代表的有理数是
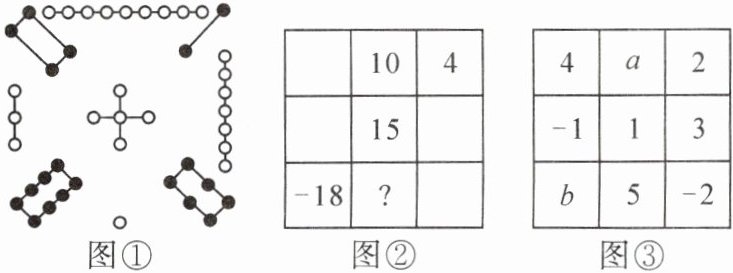
【延伸问】若图③是一个“幻方”,则a+b的值为
(教材P58活动2变式)相传大禹在治洛水的时候,洛水神龟献给大禹一本洛书,书中有一幅奇怪的图(如图①所示),这幅图用今天的符号翻译出来,就是一个三阶幻方,也就是在3×3的方阵中填入9个数,每行、每列和每条对角线上的数字和相等.如图②,这是一个三阶幻方的一部分,则图中“?”代表的有理数是
-24
.
【延伸问】若图③是一个“幻方”,则a+b的值为
-3
.
答案:
-24 【延伸问】-3
创设推理情境:请按下列要求正确填写幻方:把-4,-3,-2,-1,0,1,2,3,4这9个数除-1,1,2,3,4外填入空格中,构成幻方,并写出推理过程.
(点拨:先求出每行、每列及对角线上各数之和,再来推理)
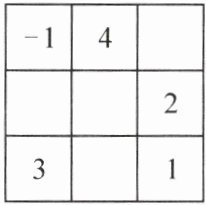
(点拨:先求出每行、每列及对角线上各数之和,再来推理)

答案:
创设推理情境:解:[(-4)+(-3)+(-2)+(-1)+0+1+2+3+4]÷3=0.第 1 行的第 3 个数是 0-(-1)-4=-3,第 3 行的第 2 个数是 0-3-1=-4,第 2 行的第 2 个数是 0-(-4)-4=0,第 2 行的第 1 个数是 0-0-2=-2.
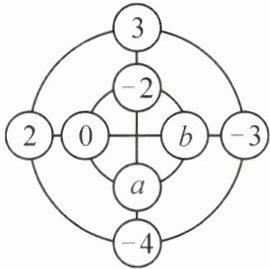
学以致用1:如图,这是一个类似于幻方的“幻圆”,将-3,2,-1,0,1,-2,3,-4分别填入图中的圆圈内,使横、竖,以及内、外两圈上的4个数字之和都相等.现已完成了部分填数,求a,b的值.

答案:
学以致用 1:解:(-3+2-1+0+1-2+3-4)÷2=-2.由题意,得 a=-2-(3-2-4)=1,b=-2-(2+0-3)=-1.
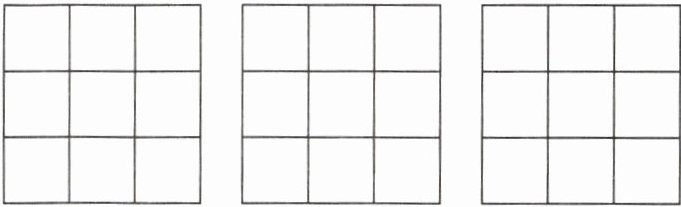
学以致用2:请将-4,-2,0,1,3,5,6,8,10这9个数,填入下面3×3的方格中,使得每行、每列、每条对角线上的三个数之和相等,构成一个三阶幻方.(至少写三种不同的填法)

答案:
学以致用 2:解:如图所示.
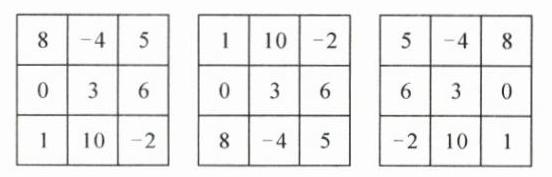
学以致用 2:解:如图所示.

查看更多完整答案,请扫码查看


