《2025年名师测控七年级数学上册人教版贵州专版》

1. 当 $ x = - 1 $ 时,代数式 $ - 3 x $ 的值为(A)
A.3
B.$ - 3 $
C.$ - 4 $
D.4

答案： A

2. 当 $ m = 1 $,$ n = - 2 $ 时,代数式 $ 2 m + n - 1 $ 的值为(D)
A.1
B.$ - 2 $
C.2
D.$ - 1 $

答案： D

3. 若 $ a = 1 $,则 $ 3 a - 2 $ 的值为1。

答案： 1

4. (教材 $ P_{80} $ 练习 $ T_{1} $ 变式)填表：
]

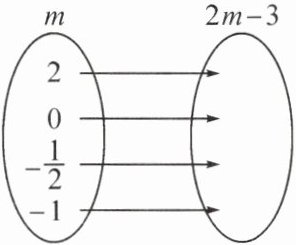
答案：

5. (2024·黔南期中)当 $ a = - 2 $,$ b = - \frac { 3 } { 2 } $ 时,求下列代数式的值。
(1)$ a + 2 b $；(2)$ a ^ { 2 } - a b + b ^ { 2 } $。

答案：
(1)原式=−2+2×(−$\frac{3}{2}$)=−2+(−3)=−5;
(2)原式=(−2)²−(−2)×(−$\frac{3}{2}$)+(−$\frac{3}{2}$)²=4−3+$\frac{9}{4}$=3$\frac{1}{4}$.

6. 数学思想 整体思想(2025·黔东南一模)已知 $ x + y = - 1010 $,则代数式 $ 5 - 2 x - 2 y $ 的值为(A)
A.2025
B.$ - 2024 $
C.2024
D.$ - 2025 $

答案： 6.A　[解析]因为5−2x−2y=5−2(x+y)，所以当x+y=−1010时，原式=5−2(x+y)=5−2×(−1010)=2025.故选:A.

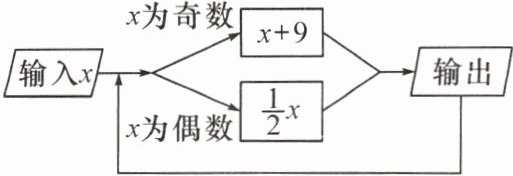
7. (2024·黔南期末)按如图所示的程序计算,若输入的 $ x $ 的值为 30,第一次得到的结果为 15,第二次得到的结果为 24,按此程序进行计算,则第 2025 次得到的结果为12。
]

答案： 7.12　[解析]第一次得到的结果为$\frac{1}{2}$×30=15；第二次得到的结果为15+9=24；第三次得到的结果为$\frac{1}{2}$×24=12；第四次得到的结果为$\frac{1}{2}$×12=6；第五次得到的结果为$\frac{1}{2}$×6=3；第六次得到的结果为3+9=12；第七次得到的结果为$\frac{1}{2}$×12=6；第八次得到的结果为$\frac{1}{2}$×6=3；...从第三次开始，每三次输出的结果为一个循环，依次为12,6,3.因为(2025−2)÷3=674...1，所以第2025次得到的结果为12，故答案为:12.

8. (2025·江苏苏州)若 $ y = x + 1 $,则代数式 $ 2 y - 2 x - 3 $ 的值为−1。
【变式 1】已知 $ x - 2 y = 3 $,则代数式 $ 6 - 2 x + 4 y $ 的值为0。
【变式 2】(2025·江苏扬州)若 $ a ^ { 2 } - 2 b + 1 = 0 $,则代数式 $ 2 a ^ { 2 } - 4 b + 3 $ 的值是1。

答案： −1　[变式1]0　[变式2]1

9. 情境题 身体质量指数 现代营养学家用身体质量指数衡量人体胖瘦程度,这个指数等于人体体重(kg)与人体身高(m)的平方的商。对于成年人来说,身体质量指数在 $ 18.5 \sim 24 $ 之间,体重适中；身体质量指数低于 $ 18.5 $,体重过轻；身体质量指数高于 $ 24 $,体重超重。
(1)设一个人的体重为 $ w $(kg),身高为 $ h $(m),则他的身体质量指数 $ p = $$\frac{w}{h^2}$；(用含 $ w $,$ h $ 的代数式表示)
(2)李老师的身高是 $ 1.70 m $,体重是 $ 60 kg $,他的体重是否适中？
当h=1.70，w=60时，p=$\frac{w}{h^2}$=$\frac{60}{1.70^2}$≈20.76.因为18.5＜20.76＜24，所以他的体重适中.

答案： 9.解:
(1)$\frac{w}{h^2}$　
(2)当h=1.70，w=60时，p=$\frac{w}{h^2}$=$\frac{60}{1.70^2}$≈20.76.因为18.5＜20.76＜24，所以他的体重适中.