第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
7. 如图是 2025 年 1 月日历,“U 型”“十字型”两个阴影图形分别覆盖其中五个数字(“U 型”“十字型”两个阴影图形可以重叠覆盖,也可以上下左右移动),设“U 型”覆盖的五个数字之和为 $S_1$,“十字型”覆盖的五个数之和为 $S_2$.
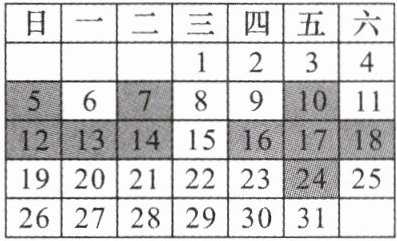
(1)“U 型”中最小的数为 13,则最大的数为
(2)设“十字型”覆盖的五个数中最中间的数为 x,则 $S_2$ 的值可以是 90 吗?请说明理由.

(1)“U 型”中最小的数为 13,则最大的数为
22
;(2)设“十字型”覆盖的五个数中最中间的数为 x,则 $S_2$ 的值可以是 90 吗?请说明理由.
不可以.理由如下:根据题意,得$x+(x-1)+(x+1)+(x-7)+(x+7)=90$.解得x=18.此时不存在“十字型”,故$S_2$的值不可以是90.
答案:
(1)22
(2)不可以.理由如下:根据题意,得$x+(x-1)+(x+1)+(x-7)+(x+7)=90$.解得x=18.此时不存在“十字型”,故$S_2$的值不可以是90.
(1)22
(2)不可以.理由如下:根据题意,得$x+(x-1)+(x+1)+(x-7)+(x+7)=90$.解得x=18.此时不存在“十字型”,故$S_2$的值不可以是90.
8. 【问题情境】
随着互联网的发展,外卖经济影响着大家的生活方式,穿梭在大街小巷的骑手给我们的生活带来了便利. 如图,某天,甲、乙两名骑手从商店 A 到同一条街道上的两个小区送外卖,由于备餐时间不同,甲先出发向东前往距离商店 3600 m 的光明小区,2 min 后乙出发向西前往距离商店 4800 m 的幸福小区,甲的平均速度为 600 m/min,乙的平均速度为 400 m/min,设骑手甲行驶的时间为 x min.

【数学思考】
(1)在两人送外卖到达目的地前,骑手甲离开商店 A 的距离为
【问题解决】
(2)在两人送外卖到达目的地前,当骑手甲距光明小区的距离等于骑手乙距商店 A 的距离时,求 x 的值.
随着互联网的发展,外卖经济影响着大家的生活方式,穿梭在大街小巷的骑手给我们的生活带来了便利. 如图,某天,甲、乙两名骑手从商店 A 到同一条街道上的两个小区送外卖,由于备餐时间不同,甲先出发向东前往距离商店 3600 m 的光明小区,2 min 后乙出发向西前往距离商店 4800 m 的幸福小区,甲的平均速度为 600 m/min,乙的平均速度为 400 m/min,设骑手甲行驶的时间为 x min.

【数学思考】
(1)在两人送外卖到达目的地前,骑手甲离开商店 A 的距离为
600x
m,骑手乙离开商店 A 的距离为400(x-2)
m;(均用含 x 的式子表示)【问题解决】
(2)在两人送外卖到达目的地前,当骑手甲距光明小区的距离等于骑手乙距商店 A 的距离时,求 x 的值.
(2)根据题意,得3600-600x=400(x-2).解得x=4.4.答:x的值为4.4.
答案:
(1)600x 400(x-2)
(2)根据题意,得3600-600x=400(x-2).解得x=4.4.答:x的值为4.4.
(1)600x 400(x-2)
(2)根据题意,得3600-600x=400(x-2).解得x=4.4.答:x的值为4.4.
9. 为节约用水,政府决定对居民用水实行三级阶梯水价:
|每户每月用水量|水费价格/(元$/m^3)$|
|不超过$ 22 m^3$|2.3|
|超过$ 22 m^3 $且不超过$ 30 m^3 $的部分|a|
|超过$ 30 m^3 $的部分|4.6|
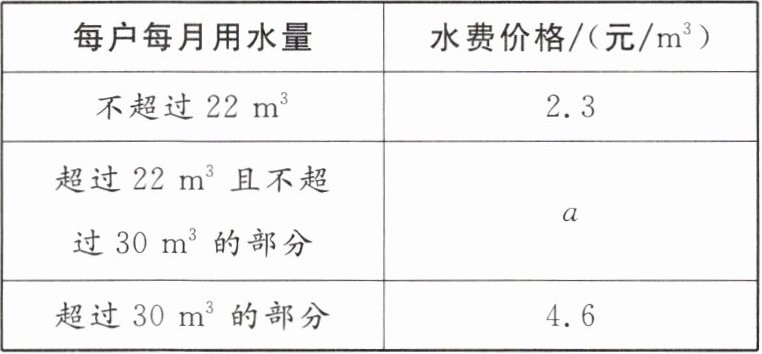
(1)若小明家今年 2 月份的用水量是$ 26 m^3,$缴费 62.6 元,请求出上表中 a 的值;
(2)在(2)的条件下,若小明家 3 月份的用水量增大,共缴费 97.6 元,请求出他家 3 月份的用水量是多少立方米.
|每户每月用水量|水费价格/(元$/m^3)$|
|不超过$ 22 m^3$|2.3|
|超过$ 22 m^3 $且不超过$ 30 m^3 $的部分|a|
|超过$ 30 m^3 $的部分|4.6|

(1)若小明家今年 2 月份的用水量是$ 26 m^3,$缴费 62.6 元,请求出上表中 a 的值;
(2)在(2)的条件下,若小明家 3 月份的用水量增大,共缴费 97.6 元,请求出他家 3 月份的用水量是多少立方米.
答案:
(1)根据题意,得(26-22)a+22×2.3=62.6.解得a=3;
(2)设小明家3月份的用水量为$x\ m^3$.因为22×2.3+(30-22)×3=74.6,而97.6>74.6,所以小明家3月份的用水量超过$30\ m^3$.根据题意,得4.6(x-30)+74.6=97.6.解得x=35.答:小明家3月份的用水量为$35\ m^3$.
(1)根据题意,得(26-22)a+22×2.3=62.6.解得a=3;
(2)设小明家3月份的用水量为$x\ m^3$.因为22×2.3+(30-22)×3=74.6,而97.6>74.6,所以小明家3月份的用水量超过$30\ m^3$.根据题意,得4.6(x-30)+74.6=97.6.解得x=35.答:小明家3月份的用水量为$35\ m^3$.
查看更多完整答案,请扫码查看


