第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
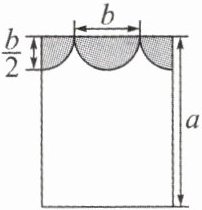
10. (2024·黔南期中)李阿姨装饰新家,为自己房间的长方形窗户选择了一种遮光的装饰物(如图所示的阴影部分),这种装饰物由一个半圆和两个四分之一圆组成.
(1)挂上这种装饰物后,窗户能射进阳光的部分的面积是多少?(用含 $a$,$b$ 的代数式表示)
(2)当 $a = 2.5m$,$b = 1m$ 时,求这扇窗户能射进阳光的部分的面积($\pi$ 取 $3.14$).
(1)挂上这种装饰物后,窗户能射进阳光的部分的面积是多少?(用含 $a$,$b$ 的代数式表示)
(2)当 $a = 2.5m$,$b = 1m$ 时,求这扇窗户能射进阳光的部分的面积($\pi$ 取 $3.14$).

答案:
解:
(1)由图可知长方形窗户的宽为b+2×$\frac{b}{2}$=2b,长为a,而阴影部分可以拼成一个半径为$\frac{b}{2}$的圆,所以窗户能射进阳光的部分的面积为2b·a-π$(\frac{b}{2})$²=2ab-$\frac{1}{4}$πb²;
(2)当a=2.5m,b=1m时,2ab-$\frac{1}{4}$πb²=2×2.5×1-$\frac{1}{4}$×3.14×1²=4.215(m²),所以这扇窗户能射进阳光的部分的面积是4.215m².
(1)由图可知长方形窗户的宽为b+2×$\frac{b}{2}$=2b,长为a,而阴影部分可以拼成一个半径为$\frac{b}{2}$的圆,所以窗户能射进阳光的部分的面积为2b·a-π$(\frac{b}{2})$²=2ab-$\frac{1}{4}$πb²;
(2)当a=2.5m,b=1m时,2ab-$\frac{1}{4}$πb²=2×2.5×1-$\frac{1}{4}$×3.14×1²=4.215(m²),所以这扇窗户能射进阳光的部分的面积是4.215m².
1. (2024·贵阳期末)如图是一个数值转换机,输入 $x$,输出 $6(x - 3)$,下面四种转换口令中正确的是(
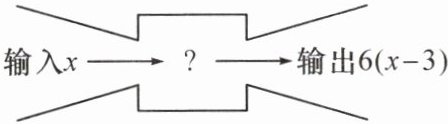
A.$x$ 的 $6$ 倍减去 $3$
B.$x$ 与 $3$ 的差的 $6$ 倍
C.$x$ 的 $6$ 倍减去 $-3$
D.$x$ 与 $-3$ 的差的 $6$ 倍
B
)
A.$x$ 的 $6$ 倍减去 $3$
B.$x$ 与 $3$ 的差的 $6$ 倍
C.$x$ 的 $6$ 倍减去 $-3$
D.$x$ 与 $-3$ 的差的 $6$ 倍
答案:
B
2. (2024·遵义期末)已知多项式 $2x + y + 3$ 的值为 $4$,则多项式 $4x + 2y + 2025$ 的值为(
A.$2025$
B.$2026$
C.$2027$
D.$2028$
C
)A.$2025$
B.$2026$
C.$2027$
D.$2028$
答案:
C 【解析】因为2x+y+3=4,所以2x+y=1,所以4x+2y=2,所以4x+2y+2025=2+2025=2027. 故选:C.
3. (2024·黔南期中)在如图所示的运算程序中,如果开始输入的 $x$ 值为 $-\frac{2}{3}$,则输出的结果为
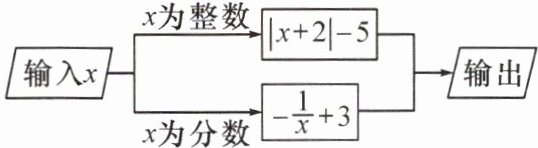
$\frac{9}{2}$
.
答案:
$\frac{9}{2}$
4. (2024·安顺期中)如图,将图①中的等边三角形剪开得到图②,图②中共有 $4$ 个等边三角形:将图②中的一个等边三角形剪开得到图③,图③中共有 $7$ 个等边三角形……如此下去,则图 $n$ 中共有
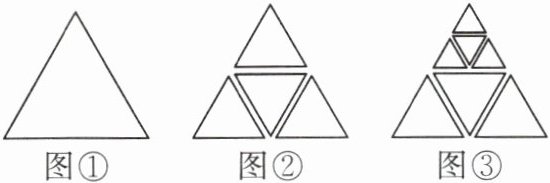
3n-2
个等边三角形.
答案:
(3n-2) 【解析】图①中共有1+3×0=1(个)等边三角形,图②中共有1+3×1=4(个)等边三角形,图③中共有1+3×2=7(个)等边三角形,图ⓝ中共有1+3(n-1)=3n-2(个)等边三角形. 故答案为:(3n-2).
5. (2024·遵义期中)甲、乙两车同时分别从两地相对开出,已知两车相距 $s$ $km$,甲车每小时行驶 $a$ $km$,乙车每小时行驶 $b$ $km$.
(1)甲车行驶完全程要
(2)用代数式表示甲、乙两车相遇用的时间 $t$(单位:$h$).当 $s = 1100$,$a = 100$,$b = 120$ 时,求 $t$ 的值.
(1)甲车行驶完全程要
$\frac{s}{a}$
$h$;乙车行驶完全程要$\frac{s}{b}$
$h$;(2)用代数式表示甲、乙两车相遇用的时间 $t$(单位:$h$).当 $s = 1100$,$a = 100$,$b = 120$ 时,求 $t$ 的值.
解:(2)由题意,得t=$\frac{s}{a+b}$h. 当s=1100,a=100,b=120时,t=$\frac{1100}{100+120}$=5(h).
答案:
解:
(1)$\frac{s}{a}$ $\frac{s}{b}$
(2)由题意,得t=$\frac{s}{a+b}$h. 当s=1100,a=100,b=120时,t=$\frac{1100}{100+120}$=5(h).
(1)$\frac{s}{a}$ $\frac{s}{b}$
(2)由题意,得t=$\frac{s}{a+b}$h. 当s=1100,a=100,b=120时,t=$\frac{1100}{100+120}$=5(h).
查看更多完整答案,请扫码查看


