《2025年名师测控七年级数学上册人教版贵州专版》

！易错点 解方程时,移项未变号或误将不移动的项变号而致错
9. 小明将方程 $2y - 1 = -3y + 6$ 进行移项变形得到 $2y - 3y = 6 - 1$,小红说小明的变形不对,则错误的原因是移项没有变号,方程正确的解是$y=\frac{7}{5}$.

答案： 移项没有变号 $y=\frac{7}{5}$

10. 某同学在解方程 $2x - 3 = □ x - 6$ 时,把□处的数字看错了,解得 $x = 3$,则该同学把□看成了(A)
A.3
B.$-3$
C.$-2$
D.2

答案： A

11.(教材 $P_{124}$ 练习 $T_3$ 变式)小雨的年龄比妈妈小 28 岁,今年妈妈的年龄正好是小雨的 5 倍,小雨今年的年龄是(A)
A.7 岁
B.8 岁
C.9 岁
D.10 岁

答案： A

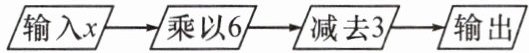
12. 新视角 程序应用(2025·四川成都)任意给一个数 $x$,按下列程序进行计算. 若输出的结果是 15,则 $x$ 的值为3.

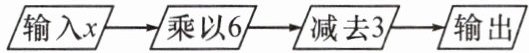
答案： 3

13. 如果 $3 - m$ 与 $2m - 5$ 互为相反数,那么 $m$ 的值为2.

答案： 2

14. 解下列方程：
(1)$x - 2 = \frac{1}{3}x + \frac{4}{3}$；
(2)$11x + 8 = 8x - 2 - 2x$.

答案： 解：
(1)移项，得$x-\frac{1}{3}x=\frac{4}{3}+2$.合并同类项，得$\frac{2}{3}x=\frac{10}{3}$.系数化为 1，得$x=5$；
(2)移项，得$11x-8x+2x=-2-8$.合并同类项，得$5x=-10$.系数化为 1，得$x=-2$.

15. 甲、乙两人同时从 A 地出发去 B 地,甲骑自行车,骑行速度为 $10\ km/h$,乙步行,行走速度为 $6\ km/h$. 当甲到达 B 地时,乙距 B 地还有 $8\ km$. 甲骑行了多长时间？A,B 两地的路程是多少？

答案： 解：设甲骑行了$x$ h，则 A，B 两地的路程是$10x$ km.根据题意，得$10x=6x+8$.解得$x=2$.所以$10x=10×2=20$.答：甲骑行了 2 h，A，B 两地的路程是 20 km.

16. 如图,将一个长方形分成六个正方形,其中最小的正方形的面积是 $1\ cm^2$,求这个长方形的面积.

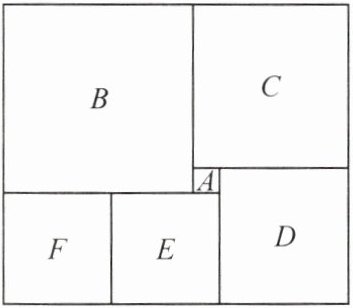
答案： 解：设正方形 E 的边长为$x$ cm，则正方形 F 的边长为$x$ cm，正方形 D 的边长为$(x+1)$cm，正方形 B 的边长为$(2x-1)$cm.根据正方形 C 的边长相等列方程，得$x+1+1=2x-1-1$.解得$x=4$.所以正方形 E 和 F 的边长为 4 cm，正方形 D 的边长为 5 cm，正方形 B 的边长为 7 cm，所以长方形的面积为$(7+4)×(4+4+5)=11×13=143(cm^{2})$.