第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
33. 如图所示,某实验小组的同学们在探究“斜面的机械效率”实验时,用弹簧测力计沿斜面匀速向上拉动物块$A$,收集了如下表中的实验数据:
|实验次数|斜面的倾斜程度|物块重力$G/N$|斜面高度$h/m$|拉力$F/N$|斜面长度$s/m$|机械效率$\eta$|
|1|较缓|$5$|$0.2$|$2.4$|$1$|$41.7\%$|
|2|较陡|$5$|$0.5$|$3.2$|$1$|$78.1\%$|
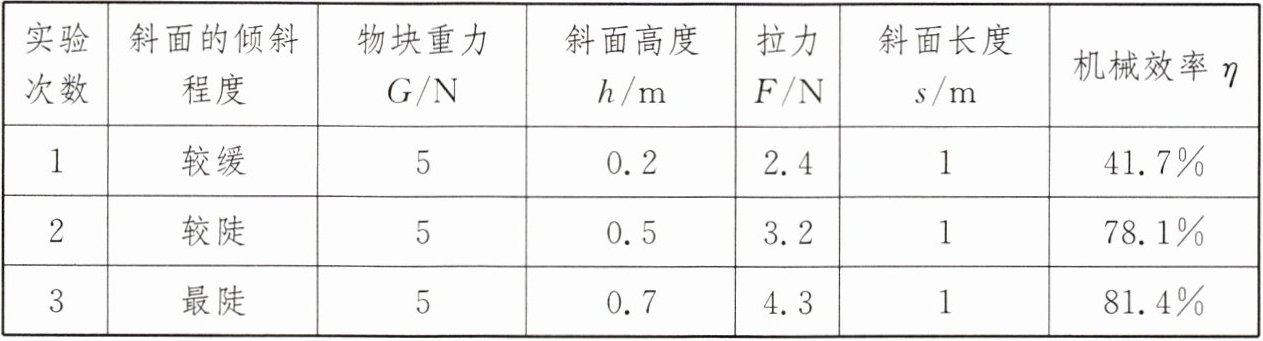
|3|最陡|$5$|$0.7$|$4.3$|$1$|$81.4\%$|\n实验时要使木板的倾斜角变大,应该把木板下面的木块向______移动(选填“左”或“右”)。分析表中的数据可得出:斜面越缓越______(选填“省”或“费”)力,斜面的机械效率越______。\n该小组又进行了第$4$次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是$0.5m和1m$,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为$4.0N$,与第二次实验相比,有用功______(选填“相同”或“不同”),而拉力做的总功______(选填“变大”或“变小”),这种情况下斜面的机械效率将______(选填“变大”或“变小”)。\n实验中,若物重、斜面长度不变,且斜面光滑,以下能正确表示拉力$F与斜面高度h$的关系的是______(填字母)。
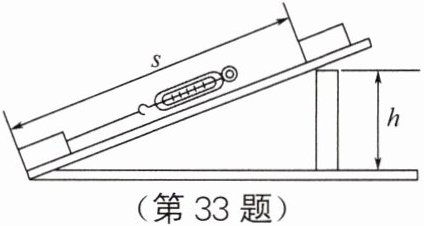

实验时要使木板的倾斜角变大,应该把木板下面的木块向
该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是0.5m和1m,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为4.0N,与第二次实验相比,有用功
实验中,若物重、斜面长度不变,且斜面光滑,以下能正确表示拉力F与斜面高度h的关系的是
|实验次数|斜面的倾斜程度|物块重力$G/N$|斜面高度$h/m$|拉力$F/N$|斜面长度$s/m$|机械效率$\eta$|
|1|较缓|$5$|$0.2$|$2.4$|$1$|$41.7\%$|
|2|较陡|$5$|$0.5$|$3.2$|$1$|$78.1\%$|

|3|最陡|$5$|$0.7$|$4.3$|$1$|$81.4\%$|\n实验时要使木板的倾斜角变大,应该把木板下面的木块向______移动(选填“左”或“右”)。分析表中的数据可得出:斜面越缓越______(选填“省”或“费”)力,斜面的机械效率越______。\n该小组又进行了第$4$次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是$0.5m和1m$,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为$4.0N$,与第二次实验相比,有用功______(选填“相同”或“不同”),而拉力做的总功______(选填“变大”或“变小”),这种情况下斜面的机械效率将______(选填“变大”或“变小”)。\n实验中,若物重、斜面长度不变,且斜面光滑,以下能正确表示拉力$F与斜面高度h$的关系的是______(填字母)。


实验时要使木板的倾斜角变大,应该把木板下面的木块向
左
移动(选填“左”或“右”)。分析表中的数据可得出:斜面越缓越省
(选填“省”或“费”)力,斜面的机械效率越小
。该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是0.5m和1m,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为4.0N,与第二次实验相比,有用功
相同
(选填“相同”或“不同”),而拉力做的总功变大
(选填“变大”或“变小”),这种情况下斜面的机械效率将变小
(选填“变大”或“变小”)。实验中,若物重、斜面长度不变,且斜面光滑,以下能正确表示拉力F与斜面高度h的关系的是
C
(填字母)。
答案:
(1)左 省 小
(2)相同 变大 变小
(3)C
(1)左 省 小
(2)相同 变大 变小
(3)C
34. 如图所示,质量为$9kg$,棱长为$5cm的正方体物块A$置于水平地面上,通过细绳系于轻质杠杆$BOC的B$端,杠杆可绕$O$点转动,且$CO = 3BO$,在$C端用F = 20N$的力竖直向下拉杠杆,使杠杆在水平位置平衡,且细绳被拉直。(细绳重力不计,$g取10N/kg$)求:
- $B端细绳的拉力F_{拉}$。
- 物体$A$对地面的压强。\n当$F$等于多少牛时,物体$A$对地面的压力恰好为零?

- $B端细绳的拉力F_{拉}$。
- 物体$A$对地面的压强。\n当$F$等于多少牛时,物体$A$对地面的压力恰好为零?

答案:
(1)求$B$端细绳的拉力$F_{拉}$
解:根据杠杆平衡条件$F_{1}L_{1}=F_{2}L_{2}$,已知$CO = 3BO$,$F = 20N$,设$BO$为$L$,则$CO$为$3L$。
可得$F_{拉}× BO=F× CO$,即$F_{拉}× L = 20N×3L$,两边同时除以$L$,解得$F_{拉}=60N$。
(2)求物体$A$对地面的压强
解:先求物体$A$的重力$G = mg$,其中$m = 9kg$,$g = 10N/kg$,则$G=9kg×10N/kg = 90N$。
物体$A$对地面的压力$F_{压}=G - F_{拉}$,$F_{拉}=60N$,所以$F_{压}=90N - 60N=30N$。
正方体棱长$a = 5cm=0.05m$,其底面积$S=a^{2}=(0.05m)^{2}=0.0025m^{2}$。
根据压强公式$p=\frac{F_{压}}{S}$,可得$p=\frac{30N}{0.0025m^{2}} = 1.2×10^{4}Pa$。
(3)求当物体$A$对地面压力恰好为零时$F$的值
解:当物体$A$对地面压力恰好为零时,$F_{拉}'=G = 90N$。
再根据杠杆平衡条件$F_{拉}'× BO=F'× CO$,$CO = 3BO$,设$BO$为$L$,则$CO$为$3L$,即$90N× L=F'×3L$,两边同时除以$3L$,解得$F' = 30N$。
综上,答案依次为:$\boldsymbol{60N}$;$\boldsymbol{1.2×10^{4}Pa}$;$\boldsymbol{30N}$。
解:根据杠杆平衡条件$F_{1}L_{1}=F_{2}L_{2}$,已知$CO = 3BO$,$F = 20N$,设$BO$为$L$,则$CO$为$3L$。
可得$F_{拉}× BO=F× CO$,即$F_{拉}× L = 20N×3L$,两边同时除以$L$,解得$F_{拉}=60N$。
(2)求物体$A$对地面的压强
解:先求物体$A$的重力$G = mg$,其中$m = 9kg$,$g = 10N/kg$,则$G=9kg×10N/kg = 90N$。
物体$A$对地面的压力$F_{压}=G - F_{拉}$,$F_{拉}=60N$,所以$F_{压}=90N - 60N=30N$。
正方体棱长$a = 5cm=0.05m$,其底面积$S=a^{2}=(0.05m)^{2}=0.0025m^{2}$。
根据压强公式$p=\frac{F_{压}}{S}$,可得$p=\frac{30N}{0.0025m^{2}} = 1.2×10^{4}Pa$。
(3)求当物体$A$对地面压力恰好为零时$F$的值
解:当物体$A$对地面压力恰好为零时,$F_{拉}'=G = 90N$。
再根据杠杆平衡条件$F_{拉}'× BO=F'× CO$,$CO = 3BO$,设$BO$为$L$,则$CO$为$3L$,即$90N× L=F'×3L$,两边同时除以$3L$,解得$F' = 30N$。
综上,答案依次为:$\boldsymbol{60N}$;$\boldsymbol{1.2×10^{4}Pa}$;$\boldsymbol{30N}$。
35. 某起重机的滑轮组结构示意如图所示,其最大载重为$5t$。起重机将$4000kg的钢板匀速提升到10m$高的桥墩上,滑轮组的机械效率为$80\%$。不计钢丝绳的重力和摩擦,$g取10N/kg$。求:
- 克服钢板重力做的功$W_{有用}$。\n钢丝绳的拉力$F$。

- 滑轮组满载时的机械效率(保留一位小数)。
- 克服钢板重力做的功$W_{有用}$。\n钢丝绳的拉力$F$。

- 滑轮组满载时的机械效率(保留一位小数)。
答案:
1. 求克服钢板重力做的功$W_{有用}$:
首先计算钢板重力$G = mg$,已知$m = 4000kg$,$g = 10N/kg$,则$G=4000kg×10N/kg = 4×10^{4}N$。
根据$W_{有用}=Gh$($h = 10m$),可得$W_{有用}=4×10^{4}N×10m=4×10^{5}J$。
2. 求钢丝绳的拉力$F$:
由图可知$n = 4$(承担物重的绳子段数)。
根据$\eta=\frac{W_{有用}}{W_{总}}$,且$W_{总}=Fs$($s = nh$),$W_{有用}=Gh$,则$\eta=\frac{Gh}{Fnh}$,变形可得$F=\frac{G}{n\eta}$。
把$G = 4×10^{4}N$,$n = 4$,$\eta = 80\%=0.8$代入,得$F=\frac{4×10^{4}N}{4×0.8}=1.25×10^{4}N$。
3. 求滑轮组满载时的机械效率:
先求动滑轮重力$G_{动}$,由$F=\frac{G + G_{动}}{n}$($F = 1.25×10^{4}N$,$G = 4×10^{4}N$,$n = 4$),可得$G_{动}=nF - G$。
$G_{动}=4×1.25×10^{4}N-4×10^{4}N=1×10^{4}N$。
最大载重$m_{max}=5t = 5000kg$,则$G_{max}=m_{max}g=5000kg×10N/kg = 5×10^{4}N$。
根据$\eta=\frac{W_{有用}}{W_{总}}=\frac{G_{max}h}{(G_{max}+G_{动})h}=\frac{G_{max}}{G_{max}+G_{动}}$($h$约掉)。
把$G_{max}=5×10^{4}N$,$G_{动}=1×10^{4}N$代入,得$\eta=\frac{5×10^{4}N}{5×10^{4}N + 1×10^{4}N}\approx83.3\%$。
综上,克服钢板重力做的功$W_{有用}=4×10^{5}J$;钢丝绳的拉力$F = 1.25×10^{4}N$;滑轮组满载时的机械效率约为$83.3\%$。
首先计算钢板重力$G = mg$,已知$m = 4000kg$,$g = 10N/kg$,则$G=4000kg×10N/kg = 4×10^{4}N$。
根据$W_{有用}=Gh$($h = 10m$),可得$W_{有用}=4×10^{4}N×10m=4×10^{5}J$。
2. 求钢丝绳的拉力$F$:
由图可知$n = 4$(承担物重的绳子段数)。
根据$\eta=\frac{W_{有用}}{W_{总}}$,且$W_{总}=Fs$($s = nh$),$W_{有用}=Gh$,则$\eta=\frac{Gh}{Fnh}$,变形可得$F=\frac{G}{n\eta}$。
把$G = 4×10^{4}N$,$n = 4$,$\eta = 80\%=0.8$代入,得$F=\frac{4×10^{4}N}{4×0.8}=1.25×10^{4}N$。
3. 求滑轮组满载时的机械效率:
先求动滑轮重力$G_{动}$,由$F=\frac{G + G_{动}}{n}$($F = 1.25×10^{4}N$,$G = 4×10^{4}N$,$n = 4$),可得$G_{动}=nF - G$。
$G_{动}=4×1.25×10^{4}N-4×10^{4}N=1×10^{4}N$。
最大载重$m_{max}=5t = 5000kg$,则$G_{max}=m_{max}g=5000kg×10N/kg = 5×10^{4}N$。
根据$\eta=\frac{W_{有用}}{W_{总}}=\frac{G_{max}h}{(G_{max}+G_{动})h}=\frac{G_{max}}{G_{max}+G_{动}}$($h$约掉)。
把$G_{max}=5×10^{4}N$,$G_{动}=1×10^{4}N$代入,得$\eta=\frac{5×10^{4}N}{5×10^{4}N + 1×10^{4}N}\approx83.3\%$。
综上,克服钢板重力做的功$W_{有用}=4×10^{5}J$;钢丝绳的拉力$F = 1.25×10^{4}N$;滑轮组满载时的机械效率约为$83.3\%$。
查看更多完整答案,请扫码查看


