《2025年能力素养与学力提升九年级物理上册苏科版》

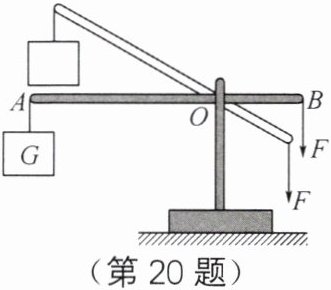
20. 如图所示,在竖直向下拉力$F$的作用下,使杠杆从水平位置将一物体缓慢匀速提升。如下表是提升物体时采集到的信息。

(1)不计杠杆自重和摩擦,杠杆处于水平静止时,求拉力$F$的大小。
(2)若实际拉力$F'为250N$,求杠杆的机械效率$\eta$。

答案： $(1)$ 求拉力$F$的大小
解：根据杠杆的平衡条件$F_{1}l_{1}=F_{2}l_{2}$（本题中$F_{1}=F$，$l_{1}=OB$，$F_{2}=G$，$l_{2}=OA$），即$F× OB = G× OA$。
已知$G = 100N$，$OA = 0.8m$，$OB = 0.4m$，将数值代入公式可得：
$F=\frac{G× OA}{OB}=\frac{100N×0.8m}{0.4m}=200N$。
$(2)$ 求杠杆的机械效率$\eta$
解：根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{F's}×100\%$。
已知$G = 100N$，$h = 0.4m$，$F' = 250N$，$s = 0.2m$，将数值代入公式可得：
$\eta=\frac{100N×0.4m}{250N×0.2m}×100\%=\frac{40J}{50J}×100\% = 80\%$。
综上，答案依次为：$(1)$$\boldsymbol{200N}$；$(2)$$\boldsymbol{80\%}$ 。

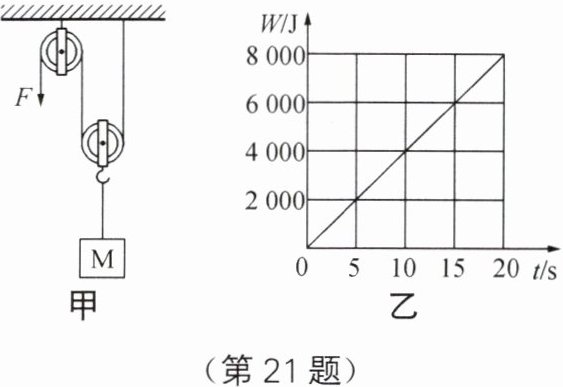
21. 用如图甲所示的滑轮组提升物体,已知被提升的物体$M质量为72kg$,绳子自由端的拉力$F将物体M以0.5m/s$的速度匀速提升。此过程中,拉力$F做的功W随时间t$的变化图像如图乙所示,不计绳重和摩擦力大小。($g取10N/kg$)求：
(1)拉力$F$做功的功率。
(2)绳子自由端拉力$F$的大小。
(3)滑轮组提升重物的机械效率。

答案： （1）求拉力$F$做功的功率
解：根据功率公式$P = \frac{W}{t}$，由图乙可知，当$t = 20s$时，$W = 8000J$，则拉力$F$做功的功率$P=\frac{W}{t}=\frac{8000J}{20s}=400W$。
（2）求绳子自由端拉力$F$的大小
解：由图甲可知，$n = 2$，则绳子自由端移动速度$v_{绳}=nv_{物}=2×0.5m/s = 1m/s$。
根据$P = Fv$（$v$为绳子自由端移动速度），可得拉力$F=\frac{P}{v_{绳}}=\frac{400W}{1m/s}=400N$。
（3）求滑轮组提升重物的机械效率
解：物体重力$G = mg = 72kg×10N/kg = 720N$。
根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{Fs}×100\%$（$s = nh$），则$\eta=\frac{G}{nF}×100\%=\frac{720N}{2×400N}×100\% = 90\%$。
综上，答案依次为：（1）$400W$；（2）$400N$；（3）$90\%$。

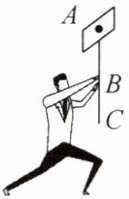
22. 如图所示是小明在学校运动会开幕式上竖直举着班牌匀速前进时的情形,将班牌视为杠杆。已知$AB = 40cm$,$BC = 20cm$,班牌受到作用在$A点的水平向左的空气阻力为10N$。若以图中$B$点作为支点,手对$C$点施加的动力为20$N$,这个力的方向是水平向左(选填“向左”或“向右”),若要用更小的力保持班牌平衡,可以适当增大$BC$之间的距离。

答案： 20　向左　增大