《2025年实验班提优训练六年级数学上册人教版》

1. 算一算。(能简算的要简算)
$\frac{5}{7} × \frac{4}{5} ÷ \frac{5}{7} × \frac{4}{7}$ $\frac{3}{4} × 56 + 45 ÷ \frac{4}{3} - 0.75$

答案： 1. $\frac{16}{35}$ 75

2. 按“减→乘→除”的运算顺序,给算式$\frac{1}{8} ÷ \frac{4}{5} - \frac{2}{3} × \frac{15}{16}$添上括号是$\frac{1}{8}÷\left[\left(\frac{4}{5}-\frac{2}{3}\right)×\frac{15}{16}\right]$。

答案： 2. $\frac{1}{8}÷\left[\left(\frac{4}{5}-\frac{2}{3}\right)×\frac{15}{16}\right]$
【提示】先算减法，即给$\left(\frac{4}{5}-\frac{2}{3}\right)$添上小括号；再算乘法，即给$\left(\frac{4}{5}-\frac{2}{3}\right)×\frac{15}{16}$添上中括号。

3. 选一选。
(1)在计算$(\frac{4}{5} + □) × \frac{5}{6}$时,若算成了$\frac{4}{5} + □ × \frac{5}{6}$,则这样得数比原来多了(C)。
A.$\frac{6}{5}$
B.$\frac{1}{3}$
C.$\frac{2}{15}$
D.$\frac{2}{3}$

答案： 3.
(1)C

(2)实验班原创 推理意识 下面是贝贝设计的一个计算程序,则输出的结果N与输入的数M相比较,( )。

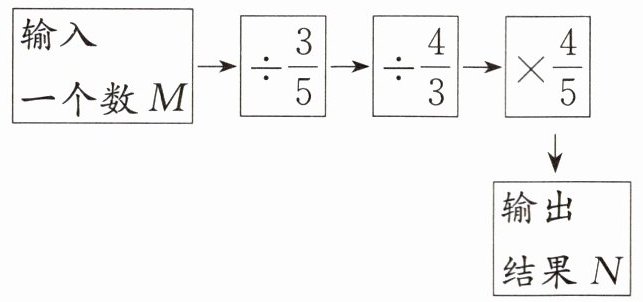
A.$N＞M$
B.$N= M$
C.$N＜M$
D.无法确定

答案：
(2)B

4. 受气候影响,过去50年青藏高原的气温平均每10年上升$\frac{8}{25}$摄氏度。照这样的速度,青藏高原的气温再上升4摄氏度需要多少年？

答案： 4.$4÷\left(\frac{8}{25}÷10\right)=125$（年）

5. 一条水渠长4400米。甲、乙两队分别从两端同时挖起,甲队开挖的速度是乙队的$\frac{6}{5}$倍。20天后,水渠顺利挖通,甲、乙两队平均每天各挖多少米？

答案： 5.乙队：$4400÷20÷\left(\frac{6}{5}+1\right)=100$（米）
甲队：$100×\frac{6}{5}=120$（米）
【提示】先根据“工作效率=工作总量÷工作时间”，计算出两队的工作效率和，再把乙队的工作效率看作1份，计算出乙队的工作效率，最后用乙队的工作效率乘$\frac{6}{5}$，计算出甲队的工作效率。
方法归纳 工程问题数量关系式
工作总量=工作效率×工作时间
工作总量=工作效率的和×工作时间
工作时间=工作总量÷工作效率
工作时间=工作总量÷工作效率的和
工作效率=工作总量÷工作时间
工作效率的和=工作总量÷工作时间

6. 小明在考试中将一个数除以$\frac{3}{5}$,错算成了除以$\frac{5}{3}$,结果是$\frac{8}{5}$。正确的结果应该是多少？

答案： 6.$\frac{8}{5}×\frac{5}{3}÷\frac{3}{5}=\frac{40}{9}$ 【提示】先根据“被除数=商×除数”，用错误的商乘错误的除数，求出正确的被除数，再用被除数除以正确的除数，求出正确的商。

【我思考】分母为1的一个数是1,分母为2的三个数的和是(2),分母为3的五个数的和是(3)……这样就把这组数分成了(1992)组,它们的和就是(1+2+3+…+1992)的和。
【我验证】$\frac{1}{1}= 1$ $\frac{1}{2}+\frac{2}{2}+\frac{1}{2}= $(2) $\frac{1}{3}+\frac{2}{3}+\frac{3}{3}+\frac{2}{3}+\frac{1}{3}= $(3) $\frac{1}{4}+\frac{2}{4}+\frac{3}{4}+\frac{4}{3}+\frac{3}{4}+\frac{2}{4}+\frac{1}{4}= $(4)
【我发现】同分母的一组分数相加得到一个整数,该整数与该组分数的分母(相同)。

答案： 7.2　3　1992　$1+2+3+\cdots+1992$　2　3　4　相同
$\frac{1}{1}+\frac{1}{2}+\frac{2}{2}+\frac{1}{2}+\frac{1}{3}+\frac{2}{3}+\frac{3}{3}+\frac{2}{3}+\frac{1}{3}+\cdots+\frac{1}{1992}+\frac{2}{1992}+\cdots+\frac{1992}{1992}+\frac{1991}{1992}+\cdots+\frac{1}{1992}$
$=1+2+3+\cdots+1992$
$=\frac{(1+1992)×1992}{2}$
$=1985028$
【提示】观察这组数据的特点，发现求这组数的和实际就是求$1+2+3+\cdots+1992$的和。