《2025年实验班提优训练六年级数学上册人教版》

1. 填一填。
(1)“女生人数是男生的$\frac{2}{5}$”是把男生人数看作单位“1”,等量关系式是男生人数×$\frac{2}{5}$=女生人数。
(2)传统文化 夏至 二十四节气之一的“夏至”是北半球一年中黑夜最短、白昼最长的一天。这一天某市的黑夜时间是白昼时间的$\frac{3}{5}$。这一天该市的黑夜是9小时。

答案： 1.
(1)男生人数 男生人数 $\frac{2}{5}$ 女生人数 【提示】根据单位“1”的判断方法，由“女生人数是男生的$\frac{2}{5}$”可知，单位“1”是男生人数；数量关系式：男生人数$×\frac{2}{5} =$女生人数。
(2)9 【提示】设这一天该市的白昼是$x$小时，则黑夜是$\frac{3}{5}x$小时。可列出方程$x+\frac{3}{5}x = 24$，解得$x = 15$，则$\frac{3}{5}x=15×\frac{3}{5}=9$。

2. 实验班原创 推理意识 实验小学成立了校园足球队,共有队员56人,女生人数是男生人数的$\frac{3}{4}$。男生和女生各有多少人？

(1)根据线段图,将题中的信息补充完整。
(2)列方程解答。
设男生有$x$人，则女生有$\frac{3}{4}x$人。
$x+\frac{3}{4}x = 56$
$x = 32$
$\frac{3}{4}x=32×\frac{3}{4}=24$

答案： 2.
(1)女生人数是男生人数的$\frac{3}{4}$
【提示】图中表示把男生人数看作单位“1”，平均分成4份，女生人数占其中的3份，故应补充“女生人数是男生人数的$\frac{3}{4}$”。
(2)设男生有$x$人，则女生有$\frac{3}{4}x$人。
$x+\frac{3}{4}x = 56$ $x = 32$
$\frac{3}{4}x=32×\frac{3}{4}=24$
【提示】用男生人数乘$\frac{3}{4}$就是女生人数，男生人数+女生人数=56，据此列方程解答。

3. 新情境 “双减”政策 “双减”政策实行后,四、五、六年级一共有148人参加数学兴趣小组。其中六年级参加的人数是五年级的$\frac{2}{3}$,四年级参加的人数是五年级的$\frac{4}{5}$,五年级有多少人参加？(用方程解)

答案： 3.设五年级有$x$人参加。
$x+\frac{2}{3}x+\frac{4}{5}x = 148$ $x = 60$
【提示】五年级参加人数+五年级参加人数$×\frac{2}{3}+$五年级参加人数$×\frac{4}{5}=$参加数学兴趣小组的总人数

4. 某小学共有学生270人,其中女生人数比男生人数的$\frac{3}{5}$多30人。这个小学女生和男生各有多少人？(用方程解)

答案： 4.设这个小学男生有$x$人。
$x+\frac{3}{5}x + 30=270$ $x = 150$
女生人数：$270-150 = 120$（人）
【提示】由“女生人数比男生人数的$\frac{3}{5}$多30人”可知，把男生人数看作单位“1”，且单位“1”未知，可设男生有$x$人。根据题中的数量关系可知，女生有$(\frac{3}{5}x + 30)$人，再根据“男生人数+女生人数=270”这一等量关系列出方程即可。

5. 甲、乙两人在银行共有存款9600元,如果两人分别取出自己存款的$\frac{2}{5}$,再从甲的存款中取出120元给乙存上,这时两人的存款数相等。乙原来的存款有多少元？(用方程解)

答案： 5.设乙原来的存款有$x$元，则甲有$(9600 - x)$元。
$(1-\frac{2}{5})x + 120=(1-\frac{2}{5})×(9600 - x)-120$
$x = 4600$
【提示】两人分别取出自己存款的$\frac{2}{5}$，则每人剩下自己存款的$(1-\frac{2}{5})$，此时“乙剩余存款+120=甲剩余存款-120”，根据这一等量关系，如果设乙原来的存款有$x$元即可列出方程，解这个方程，求出未知数$x$的值就是乙原来的存款额。

6. 一件上衣标价680元,降价至200元一件出售,仍可获利$\frac{1}{4}$。如果按标价出售,那么每件可获利多少元？

答案： 6.$200÷(1+\frac{1}{4})=160$（元） $680 - 160 = 520$（元）
【提示】把这件衣服的进价看作单位“1”，当其售价为200元时，售价是进价的$(1+\frac{1}{4})$，所以求进价，要用$200÷(1+\frac{1}{4})$。

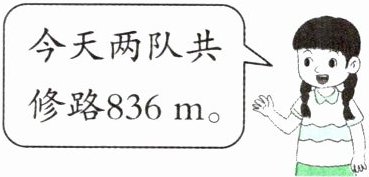
7. 修一段公路,昨天甲队比乙队多修96m,今天甲队修的米数减少了$\frac{1}{8}$,乙队修的米数增加了$\frac{1}{12}$。昨天两队共修路多少米？

答案： 7.设昨天乙队修了$x$m，则甲队修了$(x + 96)$m。
$(1+\frac{1}{12})x+(1-\frac{1}{8})×(x + 96)=836$
$x = 384$
$x + 96=384 + 96 = 480$
$384 + 480 = 864$（m）
【提示】可根据“乙队今天修路的米数+甲队今天修路的米数=836 m”列方程解答。