《2025年实验班提优训练六年级数学上册人教版》

1. 填一填。
(1)用一张长8厘米、宽6厘米的长方形纸片剪一个最大的圆,圆的面积是(28.26)平方厘米,剪掉部分的面积是(19.74)平方厘米。
(2)如下图,该图形有(2)条对称轴。图中一个圆的周长是18.84 dm。涂色部分的面积是(56.52)$dm^2,$长方形的周长是(36)dm。
(3)先把一个圆平分成若干等份,再拼成一个近似的长方形,如下图。若涂色部分的面积是$33.6 cm^2,$则圆的面积是(44.8)$cm^2。$

答案： 1.
(1)28.26 19.74 【提示】所剪的最大圆的直径等于长方形的宽，剪掉部分的面积就是长方形与圆的面积之差。
(2)2 56.52 36 【提示】圆的半径=周长÷π÷2，根据圆的半径求出2个圆的面积之和，长方形的长等于圆直径的2倍，宽等于圆的直径。
(3)44.8 【提示】涂色部分的面积等于圆面积的$\frac{3}{4}$。

2. 选一选。
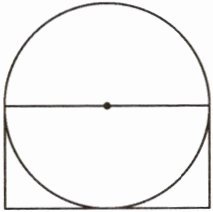
(1)如下图所示,若长方形的面积是$40 cm^2,$则圆的面积是$($A$)cm^2。$

A. 62.8
B. 125.6
C. 78.5
(2)下图中圆的面积是$18.84 cm^2,$涂色部分的面积是$($C$)cm^2。$

A. 8.84
B. 6
C. 5.16

答案： $(1)$
本题可先根据长方形面积求出圆半径的平方，再根据圆的面积公式计算圆的面积。
步骤一：分析长方形与圆的关系
设圆的半径为$r$，由图可知长方形的长为圆的直径$2r$，宽为圆的半径$r$。
根据长方形面积公式$S = 长×宽$，已知长方形面积是$40cm^2$，可得$2r× r = 40$，即$r^{2}=20$。
步骤二：计算圆的面积
根据圆的面积公式$S=\pi r^{2}$（$\pi$取$3.14$），把$r^{2}=20$代入可得：
$S = 3.14×20=62.8(cm^{2})$
所以圆的面积是$62.8cm^{2}$，答案选**A**。
$(2)$
本题可先根据圆的面积求出半径的平方，进而求出正方形的面积，最后用正方形面积减去圆的面积得到涂色部分面积。
步骤一：求圆半径的平方
已知圆的面积公式$S=\pi r^{2}$（$\pi$取$3.14$），圆的面积是$18.84cm^{2}$，则$3.14× r^{2}=18.84$，可得$r^{2}=18.84÷3.14 = 6$。
步骤二：求正方形的面积
由图可知正方形的边长等于圆的直径$2r$，根据正方形面积公式$S = 边长×边长=(2r)×(2r)=4r^{2}$，把$r^{2}=6$代入可得正方形面积为$4×6 = 24(cm^{2})$。
步骤三：求涂色部分面积
涂色部分面积$=$正方形面积$-$圆的面积，即$24 - 18.84=5.16(cm^{2})$。
所以涂色部分的面积是$5.16cm^{2}$，答案选**C**。
综上，答案依次为$(1)$ **A**；$(2)$ **C**。

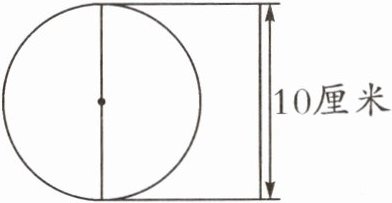
3. 如右下图,圆的面积与长方形的面积相等,长方形的宽是多少厘米?

答案： 3.$3.14×(10÷2)^{2}÷10=7.85$(厘米)【提示】圆的直径是10厘米，据此可求出圆的面积，长方形的面积与圆的面积相等，用圆的面积除以长方形的长，即可求出长方形的宽。

4. 计算右下图中涂色部分的面积。(单位:厘米)

答案： 4.$(6 + 8)×6÷2 - 3.14×6^{2}×\frac{1}{4}=13.74$(平方厘米)【提示】梯形的高等于$\frac{1}{4}$圆的半径，用梯形的面积减半径为6厘米的$\frac{1}{4}$圆的面积，就是涂色部分的面积。

5. 王大伯家用篱笆靠墙围了一个半圆形小院,小院的直径是12米。如果要扩建这个小院,把它的直径增加2米,那么这个小院的面积增加了多少平方米?

答案： 5.原来半圆半径：$12÷2 = 6$(米)扩大后半圆半径：$6 + 2÷2 = 7$(米)增加的面积：$3.14×(7^{2} - 6^{2})÷2 = 20.41$(平方米)【提示】扩建后增加部分的面积是一个半圆环形的面积，半圆环的内圆半径是$12÷2 = 6$(米)，外圆半径是$6 + 2÷2 = 7$(米)，将数据代入公式解答。

6. 如右下图,已知涂色部分的面积是$50 cm^2,$求圆环的面积。

答案： 6.$3.14×50×2 = 314(cm^{2})$【提示】涂色部分的面积=$\frac{1}{2}R^{2}-\frac{1}{2}r^{2}$

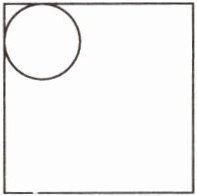
7. 如右下图,在边长为20厘米的正方形内侧有一个半径为4厘米的圆沿着正方形的四边滚动一周,这个圆滚不到的部分的面积是多少平方厘米?圆心移动的路程长多少厘米?

答案： 7.面积：(20 - 4×2×2)^{2}+[(4×2)^{2}-3.14×4^{2}]=29.76(平方厘米)圆心移动的路程：(20 - 2×4)×4 = 48(厘米)