《2025年实验班提优训练六年级数学上册人教版》

1. 选一选。
(1)下表是某消毒液的使用说明,下列说法中对“1:52”理解错误的是(D)。
|消毒液使用说明|
|衣物消毒：机洗、漂洗时,在洗涤过程中按1:52的比加入原液和水|
A.1份原液配52份水
B.水与原液的体积比是52:1
C.如果放20mL原液,那么就要放入1040mL水
D.原液占稀释后液体总质量的$\frac{1}{52}$

答案： 1.
(1)D　

(2)老师在教室多媒体上播放一部环保公益短片,当还剩5分钟的内容时,已经播放的部分和未播放部分的比是2:1,这部环保公益短片一共( )分钟。
A.10
B.15
C.20
D.25

答案：
(2)B

2. 把下面的三角形分成两部分,使它们面积的比是1:3。
]

答案：

　(答案不唯一)

3. 甲、乙、丙三个数的和是1690,已知甲数的$\frac{1}{3}等于乙数的\frac{2}{5}$,乙数的$\frac{2}{3}等于丙数的\frac{3}{7}$。甲、乙、丙三个数分别是多少？

答案： 甲数:乙数=$\frac{2}{5}$:$\frac{1}{3}$=6:5=54:45
　乙数:丙数=$\frac{3}{7}$:$\frac{2}{3}$=9:14=45:70
　甲数:乙数:丙数=54:45:70
　甲数:1690×$\frac{54}{54+45+70}$=540
　乙数:1690×$\frac{45}{54+45+70}$=450
　丙数:1690×$\frac{70}{54+45+70}$=700
[提示]根据题意，甲数×$\frac{1}{3}$=乙数×$\frac{2}{5}$，得出甲数:乙数=$\frac{2}{5}$:$\frac{1}{3}$=6:5，同样的方法可以求出乙数:丙数=$\frac{3}{7}$:$\frac{2}{3}$=9:14。两个比中都有乙数，可以利用比的基本性质把乙数化成相同的份数，可据此求出三个数的比，甲数:乙数=(6×9):(5×9)=54:45，乙数:丙数=(9×5):(14×5)=45:70，甲数:乙数:丙数=54:45:70，然后按比分配求解。

4. 修一条公路,已修的路程与未修的路程比是4:3,如果再修35千米,那么已修的路程与未修的路程比是3:1。这条公路全长多少千米？

答案： 35÷($\frac{3}{3+1}$−$\frac{4}{4+3}$)=196(千米)
[提示]已修的路程与未修的路程比是4:3，已修的路程占全长的$\frac{4}{4+3}$；再修35千米后，已修的路程与未修的路程比是3:1，此时已修的路程占全长的$\frac{3}{3+1}$，因此再修的35千米占全长的($\frac{3}{3+1}$−$\frac{4}{4+3}$)，用除法计算出这条公路的全长。

5. 甲、乙两根绳子共长22米。甲绳截去$\frac{1}{5}$后,乙绳和甲绳的长度比是3:2。甲、乙两绳原来各长多少米？

答案： (1−$\frac{1}{5}$)÷$\frac{2}{3}$=$\frac{6}{5}$
　即乙绳和甲绳原来的长度比是6:5。
　乙绳原来长:22×$\frac{6}{6+5}$=12(米)
　甲绳原来长:22×$\frac{5}{6+5}$=10(米)
[提示]甲绳截去$\frac{1}{5}$后还剩1−$\frac{1}{5}$=$\frac{4}{5}$，乙绳和现在甲绳的长度比是3:2，即甲绳的$\frac{4}{5}$是乙绳的$\frac{2}{3}$。由此可得乙绳原来是甲绳的$\frac{4}{5}$÷$\frac{2}{3}$=$\frac{6}{5}$，然后按比分配求解。

6. 有两根等长的铁丝,两根都用去了一部分。余下的铁丝中,第一根与第二根的比是4:1,第一根铁丝剩下多少米？
]

答案： (19−13)÷(4−1)=2(m)　2×4=8(m)
[提示]根据题意可知，第一根剩下的比第二根多19−13=6(m)，份数多4−1=3(份)，每份是6÷3=2(m)，这样就可以求出第一根铁丝剩下的长度。

7. 实验班原创 几何直观 如右下图,三角形ABC的面积是$30cm^2,D$是BC的中点,AE:ED= 2:1。三角形CDE的面积是多少平方厘米？

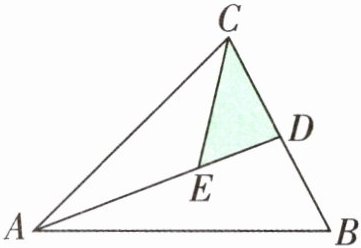
答案： 30÷2×$\frac{1}{2+1}$=5(cm²)
[提示]等底等高的三角形的面积相等，高相等的三角形的面积比就是底边长之比。