第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 填一填。
(1)把$\frac{3}{5}$米长的铁丝平均剪成4段,每段长(
(2)有$\frac{3}{4}$吨货物,甲车每次运这批货物的$\frac{1}{4}$,乙车每次运$\frac{1}{4}$吨。单独运这批货物,甲车需要(
(3)李丽$\frac{5}{12}小时走了\frac{5}{6}\ \text{km}$,她平均每小时走(
(4)一个自然数与它的倒数的差是$6\frac{6}{7}$,这个自然数是(
(5)一批木料,可以做70张课桌或90把椅子。若一张课桌和一把椅子为一套,则这批木料最多可以做(
(1)把$\frac{3}{5}$米长的铁丝平均剪成4段,每段长(
$\frac{3}{20}$
)米,每段是全长的($\frac{1}{4}$
)。(2)有$\frac{3}{4}$吨货物,甲车每次运这批货物的$\frac{1}{4}$,乙车每次运$\frac{1}{4}$吨。单独运这批货物,甲车需要(
4
)次运完,乙车需要(3
)次运完。(3)李丽$\frac{5}{12}小时走了\frac{5}{6}\ \text{km}$,她平均每小时走(
2
)km,她平均走1 km 需要($\frac{1}{2}$
)小时。(4)一个自然数与它的倒数的差是$6\frac{6}{7}$,这个自然数是(
7
)。(5)一批木料,可以做70张课桌或90把椅子。若一张课桌和一把椅子为一套,则这批木料最多可以做(
39
)套桌椅。
答案:
1.
(1)$\frac{3}{20}$ $\frac{1}{4}$ 【提示】求每段长多少米,列式为“$\frac{3}{5}÷4$”;求每段是全长的几分之几,列式为“$1÷4$”。
(2)4 3 【提示】求单独运这批货物,甲车需要运$1÷\frac{1}{4}=4$(次),乙车需要运$\frac{3}{4}÷\frac{1}{4}=3$(次)。
(3)2 $\frac{1}{2}$ 【提示】求李丽平均每小时走多少千米,列式为“$\frac{5}{6}÷\frac{5}{12}$”,求她平均走1 km需要多少小时,列式为“$\frac{5}{12}÷\frac{5}{6}$”。
(4)7 【提示】根据题意,一个自然数与它的倒数的差是$6\frac{6}{7}$,由此可知,这个自然数是7,7的倒数是$\frac{1}{7}$,$7 - \frac{1}{7}=6\frac{6}{7}$,由此解答。
(5)39 【提示】把这批木料看作单位“1”,则做一张课桌要用掉木料的$\frac{1}{70}$,做一把椅子要用掉木料的$\frac{1}{90}$,用$1÷(\frac{1}{70}+\frac{1}{90})\approx 39$,注意结果要用“去尾法”保留整数。
(1)$\frac{3}{20}$ $\frac{1}{4}$ 【提示】求每段长多少米,列式为“$\frac{3}{5}÷4$”;求每段是全长的几分之几,列式为“$1÷4$”。
(2)4 3 【提示】求单独运这批货物,甲车需要运$1÷\frac{1}{4}=4$(次),乙车需要运$\frac{3}{4}÷\frac{1}{4}=3$(次)。
(3)2 $\frac{1}{2}$ 【提示】求李丽平均每小时走多少千米,列式为“$\frac{5}{6}÷\frac{5}{12}$”,求她平均走1 km需要多少小时,列式为“$\frac{5}{12}÷\frac{5}{6}$”。
(4)7 【提示】根据题意,一个自然数与它的倒数的差是$6\frac{6}{7}$,由此可知,这个自然数是7,7的倒数是$\frac{1}{7}$,$7 - \frac{1}{7}=6\frac{6}{7}$,由此解答。
(5)39 【提示】把这批木料看作单位“1”,则做一张课桌要用掉木料的$\frac{1}{70}$,做一把椅子要用掉木料的$\frac{1}{90}$,用$1÷(\frac{1}{70}+\frac{1}{90})\approx 39$,注意结果要用“去尾法”保留整数。
2. 根据题意,选择合适的条件和算式用线连起来。
学校图书室有故事书1200册,______,图书室有科技书多少册?
|科技书比故事书多$\frac{1}{5}$|$1200×\frac{1}{5}$|
|故事书是科技书的$\frac{1}{5}$|$1200×(1-\frac{1}{5})$|
|故事书比科技书多$\frac{1}{5}$|$1200×(1+\frac{1}{5})$|
|科技书是故事书的$\frac{1}{5}$|$1200÷\frac{1}{5}$|
|科技书比故事书少$\frac{1}{5}$|$1200÷(1-\frac{1}{5})$|
|故事书比科技书少$\frac{1}{5}$|$1200÷(1+\frac{1}{5})$|
学校图书室有故事书1200册,______,图书室有科技书多少册?
|科技书比故事书多$\frac{1}{5}$|$1200×\frac{1}{5}$|
|故事书是科技书的$\frac{1}{5}$|$1200×(1-\frac{1}{5})$|
|故事书比科技书多$\frac{1}{5}$|$1200×(1+\frac{1}{5})$|
|科技书是故事书的$\frac{1}{5}$|$1200÷\frac{1}{5}$|
|科技书比故事书少$\frac{1}{5}$|$1200÷(1-\frac{1}{5})$|
|故事书比科技书少$\frac{1}{5}$|$1200÷(1+\frac{1}{5})$|
答案:


3. 计算下面各题,能简算的要简算。
$\frac{8}{9}÷(\frac{3}{4}-\frac{2}{7})$
$\frac{32}{5}÷3+\frac{13}{5}÷3$
$\frac{8}{9}÷(\frac{3}{4}-\frac{2}{7})$
$\frac{32}{5}÷3+\frac{13}{5}÷3$
答案:
$\frac{224}{117}$ 3
4. 实验班原创 模型意识 动手操作。
(1)画图表示$3÷\frac{3}{4}$的计算结果。
(2)画线段图表示出$150÷(1-\frac{1}{6})$。
(1)画图表示$3÷\frac{3}{4}$的计算结果。

(2)画线段图表示出$150÷(1-\frac{1}{6})$。
答案:
(1)
【提示】就是看3里面有几个$\frac{3}{4}$,据此画图即可。
(2)
【提示】单位“1”的量未知,且已知量“150”比单位“1”的量少$\frac{1}{6}$,据此画图即可。
(1)

【提示】就是看3里面有几个$\frac{3}{4}$,据此画图即可。
(2)

【提示】单位“1”的量未知,且已知量“150”比单位“1”的量少$\frac{1}{6}$,据此画图即可。
5. 选一选。
(1)甲数和乙数均大于0,若甲数÷乙数>甲数,则下面直线上表示乙数位置的点可能是点(
0$\quad$a$\quad$1$\quad$b$\quad$c$\quad$2$\quad$d
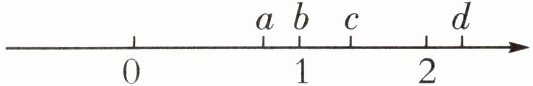
A.a
B.b
C.c
D.d
(1)甲数和乙数均大于0,若甲数÷乙数>甲数,则下面直线上表示乙数位置的点可能是点(
A
)。0$\quad$a$\quad$1$\quad$b$\quad$c$\quad$2$\quad$d
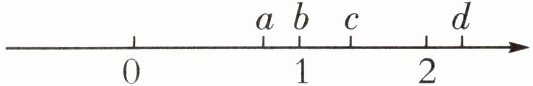
A.a
B.b
C.c
D.d
答案:
(1)A
(1)A
(2)一瓶牛奶,如果喝掉$\frac{1}{3}$后,连瓶重800 g;如果喝掉一半后,连瓶重700 g。则空瓶重( )g。
A.300
B.400
C.500
D.600
A.300
B.400
C.500
D.600
答案:
(2)B
(2)B
(3)一个水池,甲、乙两管同时打开,5小时灌满;乙、丙两管同时打开,4小时灌满。现在先开乙管6小时,还需甲、丙两管同时开2小时才能灌满。乙单独开( )小时可以灌满。
A.24
B.20
C.18
D.30
A.24
B.20
C.18
D.30
答案:
(3)B 【提示】根据题意,甲、乙的工作效率和是$\frac{1}{5}$,乙、丙的工作效率和是$\frac{1}{4}$,因此甲1小时、乙2小时、丙1小时可以完成的工作量是$\frac{1}{5}+\frac{1}{4}=\frac{9}{20}$。“现在先开乙管6小时,甲、丙合开2小时”可以看成“甲开2小时,乙开4小时,丙开2小时后,乙又开2小时”,乙又开2小时的工作量除以工作时间,得到的就是乙的工作效率,即$(1 - \frac{9}{20}×2)÷(6 - 4)=\frac{1}{20}$,故单独打开乙管灌满水池需要$1÷\frac{1}{20}=20$(小时)。
(3)B 【提示】根据题意,甲、乙的工作效率和是$\frac{1}{5}$,乙、丙的工作效率和是$\frac{1}{4}$,因此甲1小时、乙2小时、丙1小时可以完成的工作量是$\frac{1}{5}+\frac{1}{4}=\frac{9}{20}$。“现在先开乙管6小时,甲、丙合开2小时”可以看成“甲开2小时,乙开4小时,丙开2小时后,乙又开2小时”,乙又开2小时的工作量除以工作时间,得到的就是乙的工作效率,即$(1 - \frac{9}{20}×2)÷(6 - 4)=\frac{1}{20}$,故单独打开乙管灌满水池需要$1÷\frac{1}{20}=20$(小时)。
查看更多完整答案,请扫码查看


