第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
6. 跨学科 动物的睡眠时间 树袋熊,又称考拉,是澳大利亚的国宝。树袋熊和狮子都是动物界的“瞌睡鬼”。狮子每天的睡眠时间比树袋熊多几小时?

狮子:我每天的睡眠时间大约是20小时。
树袋熊:狮子的睡眠时间比我的多$\frac{1}{9}$。

狮子:我每天的睡眠时间大约是20小时。
树袋熊:狮子的睡眠时间比我的多$\frac{1}{9}$。
答案:
$20÷(1+\frac{1}{9})=18$(小时)
$20 - 18=2$(小时)
【提示】先用除法求出树袋熊每天的睡眠时间,再用减法计算。
$20 - 18=2$(小时)
【提示】先用除法求出树袋熊每天的睡眠时间,再用减法计算。
7. 周末,明明一家自驾从莆田经过福州去太姥山旅游。
(1)明明一家从莆田出发,以100千米/时的速度行驶了1小时,到达福州市,这时已行的路程比未行路程的$\frac{4}{7}$少20千米。如果以同样 的速度继续前行,再行几小时能到达太姥山?
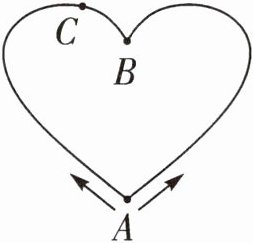
(2)太姥山景区广场有个用鹅卵石铺成的心形图案(如图),明明 和弟弟从点 A开始沿着心形的边相背而行,在距离 B点12米处 的 C点相遇,相遇时弟弟走 的路程是的$\frac {3}{4}$,这个心形鹅卵石道的周长是多少米?
(1)明明一家从莆田出发,以100千米/时的速度行驶了1小时,到达福州市,这时已行的路程比未行路程的$\frac{4}{7}$少20千米。如果以同样 的速度继续前行,再行几小时能到达太姥山?
(2)太姥山景区广场有个用鹅卵石铺成的心形图案(如图),明明 和弟弟从点 A开始沿着心形的边相背而行,在距离 B点12米处 的 C点相遇,相遇时弟弟走 的路程是的$\frac {3}{4}$,这个心形鹅卵石道的周长是多少米?

答案:
(1)$(100×1 + 20)÷\frac{4}{7}=210$(千米)
$210÷100=2.1$(小时)
【提示】根据题意,已行驶路程 + 20千米 = 未行驶路程的$\frac{4}{7}$,则未行驶的路程为$(100×1 + 20)÷\frac{4}{7}$,据此可求出未行驶的路程。再根据“时间 = 路程÷速度”即可求出以同样的速度到达太姥山还需要的时间。
(2)设相遇时明明走了x米,则弟弟走了$\frac{3}{4}x$米。
$(x+\frac{3}{4}x)÷2-\frac{3}{4}x=12$ $x=96$
$96 + 96×\frac{3}{4}=168$(米)
【提示】设相遇时明明走了x米,则弟弟走了$\frac{3}{4}x$米。明明和弟弟在距离B点12米处的C点相遇,即心形鹅卵石道周长的一半 - 弟弟走的路程 = 12米,据此可列出方程,再解这个方程即可求出明明走的路程,进而求出弟弟走的路程,明明走的路程和弟弟走的路程相加即可求出鹅卵石道的周长。
(1)$(100×1 + 20)÷\frac{4}{7}=210$(千米)
$210÷100=2.1$(小时)
【提示】根据题意,已行驶路程 + 20千米 = 未行驶路程的$\frac{4}{7}$,则未行驶的路程为$(100×1 + 20)÷\frac{4}{7}$,据此可求出未行驶的路程。再根据“时间 = 路程÷速度”即可求出以同样的速度到达太姥山还需要的时间。
(2)设相遇时明明走了x米,则弟弟走了$\frac{3}{4}x$米。
$(x+\frac{3}{4}x)÷2-\frac{3}{4}x=12$ $x=96$
$96 + 96×\frac{3}{4}=168$(米)
【提示】设相遇时明明走了x米,则弟弟走了$\frac{3}{4}x$米。明明和弟弟在距离B点12米处的C点相遇,即心形鹅卵石道周长的一半 - 弟弟走的路程 = 12米,据此可列出方程,再解这个方程即可求出明明走的路程,进而求出弟弟走的路程,明明走的路程和弟弟走的路程相加即可求出鹅卵石道的周长。
8..实验班原创 数据意识 根据统计,参加全市马拉松比赛 的运动员共有300人,男运动员人数 的$\frac {2}{5}$比女运动员人数 的$\frac {1}{4}$多29人参加马拉松比赛 的男、女运动员各有多少人?
答案:
设男运动员有x人,则女运动员有$(300 - x)$人。
$\frac{2}{5}x=(300 - x)×\frac{1}{4}+29$ $x=160$
$300 - x=300 - 160=140$
【提示】由题意知,男运动员人数$×\frac{2}{5}=$女运动员人数$×\frac{1}{4}+29$,总人数 - 男运动员人数 = 女运动员人数,根据这两个等量关系列方程解答。
$\frac{2}{5}x=(300 - x)×\frac{1}{4}+29$ $x=160$
$300 - x=300 - 160=140$
【提示】由题意知,男运动员人数$×\frac{2}{5}=$女运动员人数$×\frac{1}{4}+29$,总人数 - 男运动员人数 = 女运动员人数,根据这两个等量关系列方程解答。
9..一项工程,如果甲单独做5天后、乙再单独做7天,那么可以完成工程 的$\frac {1}{5}$;如果甲单独做7天后、乙再单独做5天,那么可以完成工程 的$\frac {1}{4}$。如果甲单独做完全部工程,那么需要多少天完成?
答案:
甲、乙的工作效率和:$(\frac{1}{5}+\frac{1}{4})÷(5 + 7)=\frac{3}{80}$
甲的工作效率:$(\frac{1}{4}-\frac{3}{80}×5)÷(7 - 5)=\frac{1}{32}$
甲单独完成需要的时间:$1÷\frac{1}{32}=32$(天)
【提示】由第一个条件“甲单独做5天”和第二个条件“甲单独做7天”可知,甲共做了$5 + 7=12$(天);再由第一个条件“乙单独做7天”和第二个条件“乙单独做5天”可知,乙共做了$5 + 7=12$(天),这样共完成的工作总量为$(\frac{1}{5}+\frac{1}{4})$,然后用“工作总量÷工作时间”即可求出甲、乙的工作效率和。而“甲单独做7天后,乙再单独做5天”相当于甲、乙合作5天后,甲再单独做$7 - 5=2$(天),由此可求出甲的工作效率,最后用“1”除以甲的工作效率即为甲单独做完全部工程需要的时间。
甲的工作效率:$(\frac{1}{4}-\frac{3}{80}×5)÷(7 - 5)=\frac{1}{32}$
甲单独完成需要的时间:$1÷\frac{1}{32}=32$(天)
【提示】由第一个条件“甲单独做5天”和第二个条件“甲单独做7天”可知,甲共做了$5 + 7=12$(天);再由第一个条件“乙单独做7天”和第二个条件“乙单独做5天”可知,乙共做了$5 + 7=12$(天),这样共完成的工作总量为$(\frac{1}{5}+\frac{1}{4})$,然后用“工作总量÷工作时间”即可求出甲、乙的工作效率和。而“甲单独做7天后,乙再单独做5天”相当于甲、乙合作5天后,甲再单独做$7 - 5=2$(天),由此可求出甲的工作效率,最后用“1”除以甲的工作效率即为甲单独做完全部工程需要的时间。
10..从甲地到乙地,$\frac {2}{5}$是上坡路,$\frac {1}{4}$平路,其余下坡路。一辆汽车从甲地开往乙地、又乙地返回甲地往返共走60千米 的上坡路。甲、乙两地相距多少千米?
答案:
$1-\frac{2}{5}-\frac{1}{4}=\frac{7}{20}$
$60÷(\frac{2}{5}+\frac{7}{20})=80$(千米)
【提示】可把全程看作单位“1”,从单位“1”里分别减去从甲地到乙地的上坡路和平路的分率,余下的就是下坡路所占的分率,同时它也是从乙地返回甲地时上坡路所占的分率。因此,往返共走了60千米的上坡路对应的分率是$(\frac{2}{5}+\frac{7}{20})$。根据除法的意义,用除法计算即可。
$60÷(\frac{2}{5}+\frac{7}{20})=80$(千米)
【提示】可把全程看作单位“1”,从单位“1”里分别减去从甲地到乙地的上坡路和平路的分率,余下的就是下坡路所占的分率,同时它也是从乙地返回甲地时上坡路所占的分率。因此,往返共走了60千米的上坡路对应的分率是$(\frac{2}{5}+\frac{7}{20})$。根据除法的意义,用除法计算即可。
11..实验班原创 应用意识 少先队大队部计划组织36名同学组成志愿小组为社区老人读报,其中男生占$\frac {4}{9}$。后来又来了几名男生,这时男生占志愿小组总人数 的$\frac {9}{19}$。后来又来了几名男生?
答案:
$36×(1-\frac{4}{9})÷(1-\frac{9}{19})-36=2$(人)
【提示】由于女生的人数始终没有变化,所以应抓住这个不变量进行分析。原来女生人数占$1-\frac{4}{9}=\frac{5}{9}$,所以女生有$36×\frac{5}{9}=20$(人);后来又来了几名男生后男生占总人数的$\frac{9}{19}$,则女生占总人数的$1-\frac{9}{19}=\frac{10}{19}$。所以后来的总人数是$20÷\frac{10}{19}=38$(人),又来的男生人数是$38 - 36=2$(人)。
举一反三 抓住不变量解题 在解答时可以抓住不变量进行分析。比如年龄问题(两人之间的年龄差始终不变)、几何形体的变形问题(体积不变)等,解答时均可从不变量的角度去分析思考。
【提示】由于女生的人数始终没有变化,所以应抓住这个不变量进行分析。原来女生人数占$1-\frac{4}{9}=\frac{5}{9}$,所以女生有$36×\frac{5}{9}=20$(人);后来又来了几名男生后男生占总人数的$\frac{9}{19}$,则女生占总人数的$1-\frac{9}{19}=\frac{10}{19}$。所以后来的总人数是$20÷\frac{10}{19}=38$(人),又来的男生人数是$38 - 36=2$(人)。
举一反三 抓住不变量解题 在解答时可以抓住不变量进行分析。比如年龄问题(两人之间的年龄差始终不变)、几何形体的变形问题(体积不变)等,解答时均可从不变量的角度去分析思考。
查看更多完整答案,请扫码查看


