第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 填一填。
(1)如下图,切拼后,这个近似的长方形的长等于圆的
(2)在一张长8cm、宽6cm的长方形纸中画出一个最大的圆,这个圆的半径是
(3)右图中正方形的周长是24厘米,这个圆的周长是
(1)如下图,切拼后,这个近似的长方形的长等于圆的
周长的一半
,宽等于圆的半径
;长方形与原来的圆相比,面积不变
,周长变大
。(填“变大”“变小”或“不变”)(2)在一张长8cm、宽6cm的长方形纸中画出一个最大的圆,这个圆的半径是
3
cm,周长是18.84
cm,面积是28.26
$cm^2。$(3)右图中正方形的周长是24厘米,这个圆的周长是
18.84
cm,圆与正方形之间的部分的面积是7.74
$cm^2。$
答案:
1.
(1)周长的一半 半径 不变 变大 [提示]切拼后,圆周长的一半分别作为长方形的两条长,而长方形的两条宽分别是圆的两条半径,所以长方形与原来的圆相比,面积不变,周长变大。
(2)3 18.84 28.26 [提示]这个圆的直径等于长方形的宽,先根据“圆的半径=直径÷2”求出它的半径,再根据“圆的周长=2πr”和“圆的面积=πr²”,分别解答即可。
(3)18.84 7.74 [提示]图中圆的直径和正方形的边长相等,先根据“正方形的边长=周长÷4”求出正方形的边长,再根据“圆的周长=πd”和“圆的面积=π(d÷2)²”,分别解答即可。
(1)周长的一半 半径 不变 变大 [提示]切拼后,圆周长的一半分别作为长方形的两条长,而长方形的两条宽分别是圆的两条半径,所以长方形与原来的圆相比,面积不变,周长变大。
(2)3 18.84 28.26 [提示]这个圆的直径等于长方形的宽,先根据“圆的半径=直径÷2”求出它的半径,再根据“圆的周长=2πr”和“圆的面积=πr²”,分别解答即可。
(3)18.84 7.74 [提示]图中圆的直径和正方形的边长相等,先根据“正方形的边长=周长÷4”求出正方形的边长,再根据“圆的周长=πd”和“圆的面积=π(d÷2)²”,分别解答即可。
2. 选一选。
(1)两个圆半径的比是2:3,它们面积的比是(
A. 2:3
B. 4:6
C. 4:9
(2)若甲圆的半径等于乙圆的直径,则甲圆的面积是乙圆的(
A. 4倍
B. 2倍
C. $\frac{1}{4}$
(3)下面两个正方形大小相等,两个正方形内的涂色部分,(
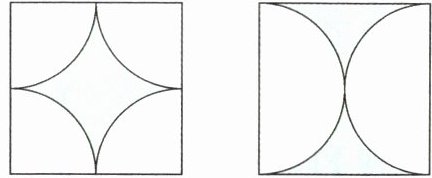
A. 周长相等,面积不相等
B. 周长和面积都相等
C. 周长不相等,面积相等
(1)两个圆半径的比是2:3,它们面积的比是(
C
)。A. 2:3
B. 4:6
C. 4:9
(2)若甲圆的半径等于乙圆的直径,则甲圆的面积是乙圆的(
A
)。A. 4倍
B. 2倍
C. $\frac{1}{4}$
(3)下面两个正方形大小相等,两个正方形内的涂色部分,(
C
)。
A. 周长相等,面积不相等
B. 周长和面积都相等
C. 周长不相等,面积相等
答案:
2.
(1)C
(2)A
(3)C
(1)C
(2)A
(3)C
3. 将一张圆形纸片剪成两个相等的半圆形纸片后,周长增加了20厘米,这个圆形纸片的面积是多少平方厘米?
答案:
3.半径:20÷2÷2=5(厘米)
面积:3.14×5²=78.5(平方厘米)
[提示]把一个圆形纸片剪成两个相等的半圆,周长增加的是圆的2条直径,以此求出圆的半径,再根据圆的面积公式计算即可。
面积:3.14×5²=78.5(平方厘米)
[提示]把一个圆形纸片剪成两个相等的半圆,周长增加的是圆的2条直径,以此求出圆的半径,再根据圆的面积公式计算即可。
4. 实验班原创 应用意识 小明想买一个直径是12厘米的披萨,商店里刚好售完,售货员提出一个建议:用总价相同的直径分别为9厘米和6厘米的同款披萨各一个来代替。就披萨的面积而言,你认为小明这样替换划算吗?
答案:
4.直径是12厘米的披萨面积:3.14×(12÷2)²=113.04(平方厘米)
直径分别为9厘米和6厘米的披萨的面积和:3.14×(9÷2)²+3.14×(6÷2)²=91.845(平方厘米)
113.04>91.845,这样替换不划算。
直径分别为9厘米和6厘米的披萨的面积和:3.14×(9÷2)²+3.14×(6÷2)²=91.845(平方厘米)
113.04>91.845,这样替换不划算。
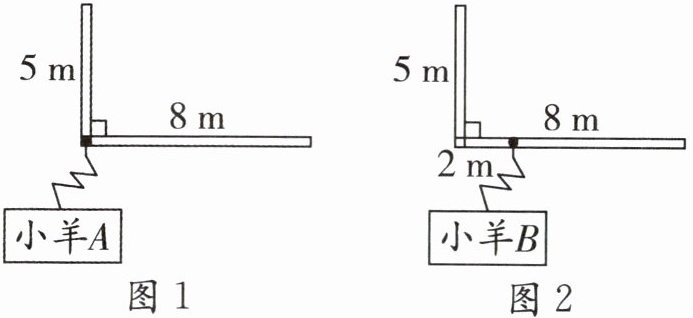
5. 如下图,院子的两堵墙分别长5m和8m,墙外是一片草地,墙上拴着一只小羊,绳长为4m。如果将小羊A和小羊B分别拴在图1和图2中的位置,那么哪只小羊所能吃到草的面积更大一些?相差多少?(结果用含有π的式子表示)

答案:
5.小羊A吃到草的面积:$\frac{3}{4}$×π×4²=12π(m²)
小羊B吃到草的面积:$\frac{1}{2}$×π×4²+$\frac{1}{4}$×π×(4−2)²=9π(m²)
12π>9π,小羊A所能吃到草的面积更大一些。
相差:12π−9π=3π(m²)
[提示]小羊A能吃到草的面积等于半径为4m 的$\frac{3}{4}$圆的面积;小羊B能吃到草的面积等于半径为4m的$\frac{1}{2}$圆的面积,再加上半径为(4−2)m的$\frac{1}{4}$圆的面积;将两个面积相减即可得到它们能吃到草的面积之差。
小羊B吃到草的面积:$\frac{1}{2}$×π×4²+$\frac{1}{4}$×π×(4−2)²=9π(m²)
12π>9π,小羊A所能吃到草的面积更大一些。
相差:12π−9π=3π(m²)
[提示]小羊A能吃到草的面积等于半径为4m 的$\frac{3}{4}$圆的面积;小羊B能吃到草的面积等于半径为4m的$\frac{1}{2}$圆的面积,再加上半径为(4−2)m的$\frac{1}{4}$圆的面积;将两个面积相减即可得到它们能吃到草的面积之差。
查看更多完整答案,请扫码查看


