第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例1 计算下图中涂色部分的面积。(单位:厘米)
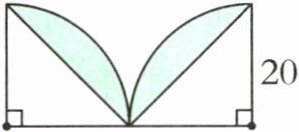
解析
按照一般思路,可以先求出$\frac{1}{4}$个圆的面积(扇形的面积)和空白三角形的面积,然后把它们的面积相减求差后乘2。也可以将右半部分平移,与左半部分拼成一个半圆,那么涂色部分的面积就等于半圆的面积减中间大三角形的面积。
答案:方法一:$(3.14×20^{2}×\frac{1}{4}-20×20÷2)×2= 228$(平方厘米)
方法二:$3.14×20^{2}×\frac{1}{2}-20×2×20×\frac{1}{2}= 228$(平方厘米)
答:涂色部分的面积是228平方厘米。
小结
计算组合图形的面积时,要观察图中组合图形是由哪些基本图形组合或分割而成的,再根据分割法、平移法等方法进行适当变形。

解析
按照一般思路,可以先求出$\frac{1}{4}$个圆的面积(扇形的面积)和空白三角形的面积,然后把它们的面积相减求差后乘2。也可以将右半部分平移,与左半部分拼成一个半圆,那么涂色部分的面积就等于半圆的面积减中间大三角形的面积。
答案:方法一:$(3.14×20^{2}×\frac{1}{4}-20×20÷2)×2= 228$(平方厘米)
方法二:$3.14×20^{2}×\frac{1}{2}-20×2×20×\frac{1}{2}= 228$(平方厘米)
答:涂色部分的面积是228平方厘米。
小结
计算组合图形的面积时,要观察图中组合图形是由哪些基本图形组合或分割而成的,再根据分割法、平移法等方法进行适当变形。
答案:
方法一:$(3.14×20^{2}×\frac{1}{4}-20×20÷2)×2$
$=(3.14×400×\frac{1}{4}-400÷2)×2$
$=(314 - 200)×2$
$=114×2$
$=228$(平方厘米)
方法二:$3.14×20^{2}×\frac{1}{2}-20×2×20×\frac{1}{2}$
$=3.14×400×\frac{1}{2}-40×20×\frac{1}{2}$
$=628 - 400$
$=228$(平方厘米)
答:涂色部分的面积是228平方厘米。
$=(3.14×400×\frac{1}{4}-400÷2)×2$
$=(314 - 200)×2$
$=114×2$
$=228$(平方厘米)
方法二:$3.14×20^{2}×\frac{1}{2}-20×2×20×\frac{1}{2}$
$=3.14×400×\frac{1}{2}-40×20×\frac{1}{2}$
$=628 - 400$
$=228$(平方厘米)
答:涂色部分的面积是228平方厘米。
1. 如右下图,已知大正方形的边长为6 cm,小正方形的边长为4 cm,求涂色部分的面积。
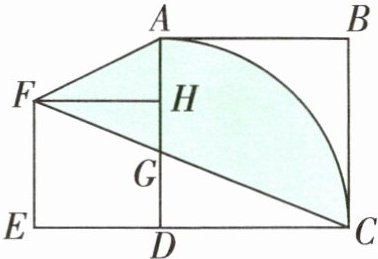

答案:
1.(4+6)×4÷2+3.14×6²÷4-4×(4+6)÷2=28.26(cm²)
【提示】涂色部分的面积=梯形ADEF的面积+扇形ACD的面积-三角形FCE的面积
【提示】涂色部分的面积=梯形ADEF的面积+扇形ACD的面积-三角形FCE的面积
例2 如右图,正方形的面积是$60cm^{2}$,求涂色部分的面积。

解析
连接正方形的对角线(如右下图),从图中可以看出正方形的对角线是扇形的半径,设对角线的长为r cm,则$r^{2}= S_{正}×2$,这样可以求出扇形的面积,用扇形的面积减去正方形的面积就是涂色部分的面积。
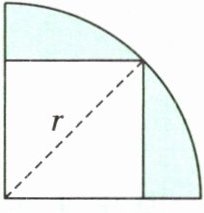
答案:设对角线的长为r cm。
$r^{2}= S_{正}×2= 60×2= 120(cm^{2})$
$\frac{1}{4}×3.14×120-60= 34.2(cm^{2})$
答:涂色部分的面积是$34.2cm^{2}$。
小结
求圆或圆环面积,不一定非要知道R和r的具体数值,若知道$R^{2}$、$r^{2}或R^{2}-r^{2}$,则用代换法就可以计算。

解析
连接正方形的对角线(如右下图),从图中可以看出正方形的对角线是扇形的半径,设对角线的长为r cm,则$r^{2}= S_{正}×2$,这样可以求出扇形的面积,用扇形的面积减去正方形的面积就是涂色部分的面积。

答案:设对角线的长为r cm。
$r^{2}= S_{正}×2= 60×2= 120(cm^{2})$
$\frac{1}{4}×3.14×120-60= 34.2(cm^{2})$
答:涂色部分的面积是$34.2cm^{2}$。
小结
求圆或圆环面积,不一定非要知道R和r的具体数值,若知道$R^{2}$、$r^{2}或R^{2}-r^{2}$,则用代换法就可以计算。
答案:
设正方形对角线的长为$r$cm。
$r^{2}=60×2=120$($cm^{2}$)
$\frac{1}{4}×3.14×120 - 60 = 34.2$($cm^{2}$)
答:涂色部分的面积是$34.2cm^{2}$。
$r^{2}=60×2=120$($cm^{2}$)
$\frac{1}{4}×3.14×120 - 60 = 34.2$($cm^{2}$)
答:涂色部分的面积是$34.2cm^{2}$。
2. 如右下图,四边形ABCD是正方形,求涂色部分的面积。(单位:cm)
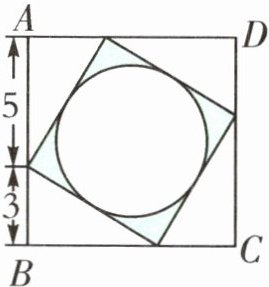

答案:
2.内部正方形的面积:(5+3)²-5×3÷2×4=34(cm²)
圆的面积:3.14×(34÷4)=26.69(cm²)
涂色部分的面积:34-26.69=7.31(cm²)
【提示】先算出内部正方形的面积,设圆的半径为r,则4r²=内部正方形的面积,由此求出圆的面积,进而求出涂色部分的面积。
圆的面积:3.14×(34÷4)=26.69(cm²)
涂色部分的面积:34-26.69=7.31(cm²)
【提示】先算出内部正方形的面积,设圆的半径为r,则4r²=内部正方形的面积,由此求出圆的面积,进而求出涂色部分的面积。
查看更多完整答案,请扫码查看


