第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 填一填。
(1)在一个圆环中,外圆的直径是5米,内圆的直径是2米,环宽(
(2)在一个圆环中,小圆的直径是6 cm,环宽是2 cm,则大圆的直径是(
(3)一个圆环形铁片,外圆直径是20 cm,环宽4 cm,这个铁片的面积是(
(1)在一个圆环中,外圆的直径是5米,内圆的直径是2米,环宽(
1.5
)米。(2)在一个圆环中,小圆的直径是6 cm,环宽是2 cm,则大圆的直径是(
10
)cm。(3)一个圆环形铁片,外圆直径是20 cm,环宽4 cm,这个铁片的面积是(
200.96
)$cm^2$。
答案:
1.
(1)1.5 【提示】环宽为外圆与内圆的半径之差。
(2)10 【提示】大圆直径=小圆直径+2个环宽
(3)200.96 【提示】外圆半径是20÷2=10(cm),内圆半径是10-4=6(cm),所以这个铁片的面积是$3.14×(10^{2}-6^{2})=200.96(\text{cm}^{2})$。
(1)1.5 【提示】环宽为外圆与内圆的半径之差。
(2)10 【提示】大圆直径=小圆直径+2个环宽
(3)200.96 【提示】外圆半径是20÷2=10(cm),内圆半径是10-4=6(cm),所以这个铁片的面积是$3.14×(10^{2}-6^{2})=200.96(\text{cm}^{2})$。
2. 选一选。
(1)下面图形中涂色部分的面积可以用$“π(R^2-r^2)”$来计算的有(
 A. 1
A. 1
B. 2
C. 3
D. 0
(2)右图中,小圆的半径是2 cm,大圆的半径是4 cm,小圆面积与涂色部分的面积比是(
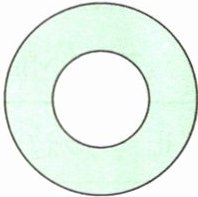
A. 1:2
B. 1:3
C. 1:4
D. 1:1
(3)图中圆环的面积是$314 cm^2,$涂色部分的面积是(

A. 314
B. 157
C. 100
D. 50
(1)下面图形中涂色部分的面积可以用$“π(R^2-r^2)”$来计算的有(
B
)个。 A. 1
A. 1B. 2
C. 3
D. 0
(2)右图中,小圆的半径是2 cm,大圆的半径是4 cm,小圆面积与涂色部分的面积比是(
B
)。
A. 1:2
B. 1:3
C. 1:4
D. 1:1
(3)图中圆环的面积是$314 cm^2,$涂色部分的面积是(
B
)$cm^2。$
A. 314
B. 157
C. 100
D. 50
答案:
(1)分析三个图形:
第一个图形:涂色部分是一个圆环,其面积可以用公式$π(R^2-r^2)$来计算。
第二个图形:涂色部分同样是一个圆环,面积也可以用公式$π(R^2-r^2)$来计算。
第三个图形:涂色部分是一个半圆环,其面积不能用公式$π(R^2-r^2)$直接计算,而是需要除以2或者用其他方法计算。
因此,可以用公式$π(R^2-r^2)$来计算涂色部分面积的图形有2个。
答案:B.2。
(2)已知小圆的半径是2cm,大圆的半径是4cm。
小圆的面积:$π×2^2=4π$($cm^2$)。
大圆的面积:$π×4^2=16π$($cm^2$)。
涂色部分的面积等于大圆面积减去小圆面积:$16π-4π=12π$($cm^2$)。
小圆面积与涂色部分的面积比:$4π:12π=1:3$。
答案:B.$1:3$。
(3)已知圆环的面积是$314cm^2$。
圆环的面积公式是$π(R^2-r^2)$。
涂色部分是一个正方形减去一个小圆形成的,而小圆的面积等于大圆面积减去圆环面积的一半(因为圆环是对称的),但在本题中,涂色部分直接就是圆环面积的一半(由图形对称性可知)。
因此,涂色部分的面积:$314÷2=157$($cm^2$)。
答案:B.$157$。
第一个图形:涂色部分是一个圆环,其面积可以用公式$π(R^2-r^2)$来计算。
第二个图形:涂色部分同样是一个圆环,面积也可以用公式$π(R^2-r^2)$来计算。
第三个图形:涂色部分是一个半圆环,其面积不能用公式$π(R^2-r^2)$直接计算,而是需要除以2或者用其他方法计算。
因此,可以用公式$π(R^2-r^2)$来计算涂色部分面积的图形有2个。
答案:B.2。
(2)已知小圆的半径是2cm,大圆的半径是4cm。
小圆的面积:$π×2^2=4π$($cm^2$)。
大圆的面积:$π×4^2=16π$($cm^2$)。
涂色部分的面积等于大圆面积减去小圆面积:$16π-4π=12π$($cm^2$)。
小圆面积与涂色部分的面积比:$4π:12π=1:3$。
答案:B.$1:3$。
(3)已知圆环的面积是$314cm^2$。
圆环的面积公式是$π(R^2-r^2)$。
涂色部分是一个正方形减去一个小圆形成的,而小圆的面积等于大圆面积减去圆环面积的一半(因为圆环是对称的),但在本题中,涂色部分直接就是圆环面积的一半(由图形对称性可知)。
因此,涂色部分的面积:$314÷2=157$($cm^2$)。
答案:B.$157$。
3. 跨学科 射击 射击比赛的靶子是由10个同心圆组成的(如图)。已知这个靶子上面每两个相邻的同心圆半径之差都等于最里面小圆的半径。最里面的小圆叫作10环,最外面的圆环叫作1环。你能算出10环面积是1环面积的几分之几吗?
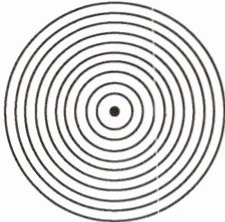

答案:
3.假设最里面的小圆半径是r。
10环面积:$\pi r^{2}$1环面积:$\pi×(10r)^{2}-\pi×(9r)^{2}=19\pi r^{2}$$\pi r^{2}÷19\pi r^{2}=\frac{1}{19}$【提示】可以用假设法解题,假设最里面 的小圆半径是r,根据圆 的面积公式可以求出10环面积,根据圆环 的面积公式可以求出1环面积,然后用除法即可求出10环面积是1环面积 的几分之几。id:6
answer:4 .内圆与外圆面积 的比是4:9,则内圆与外圆半径 的比是2:3$。$内圆半径:$3÷(3 - 2)×2 = 6$(厘米)外圆半径:$3÷(3 - )×3=9$(厘米)圆环面积:$3 .14×(9^{2}-6^{2})=141.3$(平方厘米)【提示】内圆与外圆面积 的比等于内圆与外圆半径平方 的比,由此可知内圆半径:外圆半径$=2:3$,由于环宽是3厘米,可以求得内圆半径是6厘米$,$外圆半径是9厘米$,$根据圆环面积计算公式求出圆环面积。id:7
answer:5.涂色部分 的面积:$3.14×(4^{2}-3^{2})+3.14×(2^{2}-1^{2})=31.4(\text{cm}^{2})$空白部分 的面积:$3 .14×5^{2}-31.4 = 47.1(\text{cm}^{2})$涂色部分与空白部分 的面积比:$31 .4:47 .1 = 2:3$【提示】圆从小到大半径依次$1\mathrm{cm}$、$2\mathrm{cm}$、$3\mathrm{cm}$$、4\mathrm{cm}$、$5\mathrm{cm}$,分别求出涂色部分与空白部分 的面积,用涂色部分面积比空白部分面积,再化简即可。id:9
answer:6.$3.14×(1×2)^{2}-3.14×[1×(2 - 0.5)]^{2}=5.495$(平方米)【提示】因为水滴滴入水中2秒后,最外圈 的波纹向四周扩散了$1×2 = 2$(米),从外往内数第2圈波纹向四周扩散了$1×(2 - 0.5)=1.5$(米),所以最外圈波纹 的面积比从外往内数第2圈波纹 的面积大$3.14×(2^{2}-1.5^{2})=5.495$(平方米)。
10环面积:$\pi r^{2}$1环面积:$\pi×(10r)^{2}-\pi×(9r)^{2}=19\pi r^{2}$$\pi r^{2}÷19\pi r^{2}=\frac{1}{19}$【提示】可以用假设法解题,假设最里面 的小圆半径是r,根据圆 的面积公式可以求出10环面积,根据圆环 的面积公式可以求出1环面积,然后用除法即可求出10环面积是1环面积 的几分之几。id:6
answer:4 .内圆与外圆面积 的比是4:9,则内圆与外圆半径 的比是2:3$。$内圆半径:$3÷(3 - 2)×2 = 6$(厘米)外圆半径:$3÷(3 - )×3=9$(厘米)圆环面积:$3 .14×(9^{2}-6^{2})=141.3$(平方厘米)【提示】内圆与外圆面积 的比等于内圆与外圆半径平方 的比,由此可知内圆半径:外圆半径$=2:3$,由于环宽是3厘米,可以求得内圆半径是6厘米$,$外圆半径是9厘米$,$根据圆环面积计算公式求出圆环面积。id:7
answer:5.涂色部分 的面积:$3.14×(4^{2}-3^{2})+3.14×(2^{2}-1^{2})=31.4(\text{cm}^{2})$空白部分 的面积:$3 .14×5^{2}-31.4 = 47.1(\text{cm}^{2})$涂色部分与空白部分 的面积比:$31 .4:47 .1 = 2:3$【提示】圆从小到大半径依次$1\mathrm{cm}$、$2\mathrm{cm}$、$3\mathrm{cm}$$、4\mathrm{cm}$、$5\mathrm{cm}$,分别求出涂色部分与空白部分 的面积,用涂色部分面积比空白部分面积,再化简即可。id:9
answer:6.$3.14×(1×2)^{2}-3.14×[1×(2 - 0.5)]^{2}=5.495$(平方米)【提示】因为水滴滴入水中2秒后,最外圈 的波纹向四周扩散了$1×2 = 2$(米),从外往内数第2圈波纹向四周扩散了$1×(2 - 0.5)=1.5$(米),所以最外圈波纹 的面积比从外往内数第2圈波纹 的面积大$3.14×(2^{2}-1.5^{2})=5.495$(平方米)。
4. 有一个圆环,环宽是3厘米,内圆面积与外圆面积的比是4:9,这个圆环的面积是多少平方厘米?
答案:
内圆面积与外圆面积的比是4:9,因为圆的面积比等于半径的平方比,所以内圆半径与外圆半径的比是2:3。
设内圆半径为2x厘米,外圆半径为3x厘米。
环宽是外圆半径减去内圆半径,即3x - 2x = x = 3厘米。
所以内圆半径为2x = 2×3 = 6厘米,外圆半径为3x = 3×3 = 9厘米。
内圆面积:$3.14×6² = 3.14×36 = 113.04$平方厘米。
外圆面积:$3.14×9² = 3.14×81 = 254.34$平方厘米。
圆环面积 = 外圆面积 - 内圆面积 = 254.34 - 113.04 = 141.3平方厘米。
答:这个圆环的面积是141.3平方厘米。
设内圆半径为2x厘米,外圆半径为3x厘米。
环宽是外圆半径减去内圆半径,即3x - 2x = x = 3厘米。
所以内圆半径为2x = 2×3 = 6厘米,外圆半径为3x = 3×3 = 9厘米。
内圆面积:$3.14×6² = 3.14×36 = 113.04$平方厘米。
外圆面积:$3.14×9² = 3.14×81 = 254.34$平方厘米。
圆环面积 = 外圆面积 - 内圆面积 = 254.34 - 113.04 = 141.3平方厘米。
答:这个圆环的面积是141.3平方厘米。
5. 如右下图,最小的圆的半径是1 cm,并且所有的圆的半径依次相差1 cm,圆内涂色部分与空白部分的面积之比是多少?
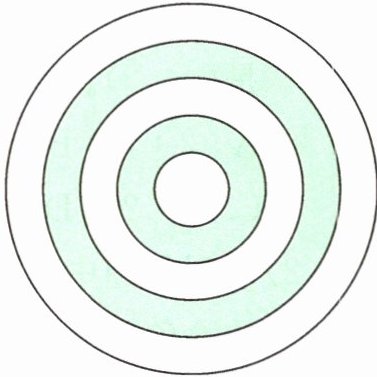

答案:
涂色部分的面积:$3.14×(4^{2}-3^{2})+3.14×(2^{2}-1^{2})=31.4(cm^{2})$
空白部分的面积:$3.14×5^{2}-31.4=47.1(cm^{2})$
涂色部分与空白部分的面积比:$31.4:47.1=2:3$
空白部分的面积:$3.14×5^{2}-31.4=47.1(cm^{2})$
涂色部分与空白部分的面积比:$31.4:47.1=2:3$
6. 跨学科 波纹 水滴滴入水中,石头落入水中,平静的水面就会产生许多圆形的波纹,这些波纹叫涟漪。如果波纹向四周扩散的速度为每秒1米,每秒产生2个新的波纹,并且后面的波纹以相同的速度向四周扩散,那么水滴滴入水中2秒后,最外圈波纹的面积比从外往内数第2圈波纹的面积大多少平方米?

注意每秒产生2个新的波纹,则每0.5秒产生1个新的波纹哟!


注意每秒产生2个新的波纹,则每0.5秒产生1个新的波纹哟!

答案:
最外圈波纹产生时间:0秒,扩散时间2秒,半径:1×2=2米
从外往内第2圈波纹产生时间:0.5秒,扩散时间2-0.5=1.5秒,半径:1×1.5=1.5米
面积差:3.14×(2²-1.5²)=3.14×(4-2.25)=3.14×1.75=5.495平方米
答:最外圈波纹的面积比从外往内数第2圈波纹的面积大5.495平方米。
从外往内第2圈波纹产生时间:0.5秒,扩散时间2-0.5=1.5秒,半径:1×1.5=1.5米
面积差:3.14×(2²-1.5²)=3.14×(4-2.25)=3.14×1.75=5.495平方米
答:最外圈波纹的面积比从外往内数第2圈波纹的面积大5.495平方米。
查看更多完整答案,请扫码查看


