《2025年实验班提优训练六年级数学上册人教版》

1. 填一填。
(1)计算$\frac {5}{7}-\frac {3}{4}×\frac {1}{3}$时,先算乘法,再算减法。
(2)计算$(\frac {3}{4}-\frac {5}{7})×\frac {1}{3}$时,先算减法,再算乘法。

答案： 1.
(1)乘 减
(2)减 乘

2. 计算下面各题。
$\frac {3}{8}×\frac {8}{9}+\frac {5}{12}$
$12-\frac {8}{15}×\frac {3}{4}$
$\frac {13}{22}-\frac {1}{2}×\frac {10}{11}$
$\frac {6}{7}×(\frac {5}{6}+\frac {1}{4})$

答案： 2.$\frac{3}{4}$ $11\frac{3}{5}$ $\frac{3}{22}$ $\frac{13}{14}$

3. 一根绳子长3米,第一次截去全长的$\frac {2}{3}$,第二次截去$\frac {1}{3}$米。还剩下多少米？

答案： 3.$3-3×\frac{2}{3}-\frac{1}{3}=\frac{2}{3}$(米)
【提示】第一次截去全长的$\frac{2}{3}$,因此第一次截去$3×\frac{2}{3}=2$(米),用全长—第一次截去的长度—第二次截去的长度=剩下的长度。
易错警示 分率与数量的辨析
分率是用于描述两个数量之间的关系，通常以分数的形式出现，不带单位名称。如本题中的“$\frac{2}{3}$”就是分率；而数量则用于描述一个事物的多少，通常以整数、小数或分数的形式出现，并且会带有单位名称。如本题中的“$\frac{1}{3}$米”就是具体的数量。

4. 新情境 C919 客机构造 C919 大型客机是中国首款完全按照最新国际适航标准研制的单通道大型干线客机,具有中国完全自主知识产权。C919 大型客机的翼展约36米,机身的长度比翼展长$\frac {1}{12}$。C919 大型客机的机身约长多少米？

答案： 4.$36+36×\frac{1}{12}=39$(米)
【提示】用C919大型客机的翼展长度加上翼展长度的$\frac{1}{12}$,就是机身的长度。

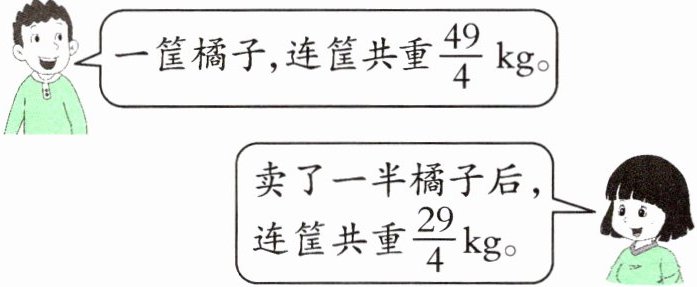
5. 筐和原来橘子的质量分别是多少千克？

答案： 5.原来橘子的质量:$(\frac{49}{4}-\frac{29}{4})×2=10$(kg)
筐的质量:$\frac{49}{4}-10=\frac{9}{4}$(kg)
【提示】用原来橘子和筐的总质量减去卖了一半橘子后橘子和筐的总质量,得到原来橘子质量的一半,进而算出原来橘子的质量和筐的质量。

6. 商店运来800千克白糖,第一天卖出总数的$\frac {1}{5}$,第二天比第一天多卖出总数的$\frac {1}{8}$,第三天闭店时还剩下总数的$\frac {2}{5}$没卖出。第三天卖出白糖多少千克？

答案： 6.$\frac{1}{5}+\frac{1}{8}+\frac{1}{5}=\frac{21}{40}$
$1-\frac{2}{5}-\frac{21}{40}=\frac{3}{40}$
$800×\frac{3}{40}=60$(千克)
【提示】先计算出第三天卖出的白糖质量对应的分率,再求解。

7. 实验班原创 运算能力 巧算：$(1-\frac {1}{2})×(1-\frac {1}{3})×(1-\frac {1}{4})×... ×(1-\frac {1}{100})$。

答案： 7.$\frac{1}{100}$ 【提示】$(1-\frac{1}{2})×(1-\frac{1}{3})×(1-\frac{1}{4})×\cdots×(1-\frac{1}{100})=\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{99}{100}=\frac{1}{100}$