《2025年名校课堂七年级数学上册北师大版》

13. 若关于$x$的一元一次方程$2x^a + m = 4$的解为$x = 1$，则$a + m$的值为(D)

A.$9$
B.$8$
C.$4$
D.$3$

答案： 13.D

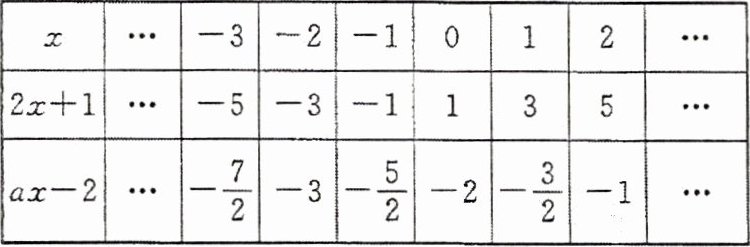
14. 观察下表，写出关于$x$的方程$2x + 1 = ax - 2$的解是x = - 2.

答案： 14.$x = - 2$

15. 清华附中校本经典题 古埃及人的“纸草书”中记录了一个数学问题：一个数，它的三分之二，它的一半，它的七分之一，它的全部，加起来总共是33.若设这个数是$x$，则可列方程为\frac{2}{3}x + \frac{1}{2}x + \frac{1}{7}x + x = 33.

答案： 15.$\frac{2}{3}x + \frac{1}{2}x + \frac{1}{7}x + x = 33$

16. 已知方程$(|m| - 2)x^2 - (m + 2)x - 6 = 0$是关于$x$的一元一次方程.
(1)求$m$的值.
(2)判断$x = 3$与$x = -\frac{3}{2}$是不是该方程的解.

答案： 16.解：
(1)$\because$方程$(|m| - 2)x^{2} - (m + 2)x - 6 = 0$是关于$x$的一元一次方程，$\therefore|m| - 2 = 0,m + 2 \neq 0$．$\therefore m = 2$.
(2)由
(1)知原方程为$- 4x - 6 = 0$.当$x = 3$时，$- 4x - 6 = - 18 \neq 0$;当$x = - \frac{3}{2}$
时，$- 4x - 6 = 0$，$\therefore x = - \frac{3}{2}$是该方程的解，$x = 3$不是该方程的解．

17. 某校七年级的一名学生做作业时，不慎将墨水瓶打翻，使一道题只看到如下字样：“某中学举办了足球比赛，计分规则为胜一场积2分，平一场积1分，负一场积0分，某班参加14场比赛始终保持不败的纪录，共得22分，求?”请你将这道题补充完整，并列出方程.

答案： 17.解：答案不唯一，如补充：该班胜了多少场比赛．设该班胜了$x$场比赛．根据题意，得$2x + (14 - x) = 22$.

18. (教材P138习题T4变式)在数学课上，老师展示了下列问题.
中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有这样一个问题：“今有三人共车，二车空；二人共车，九人步，问人和车各几何?”这个题的意思是：今有若干人乘车.若每3人乘一辆车，则余2辆空车；若每2人乘一辆车，则余9人需步行.问共有多少辆车？多少人？
某小组选择用一元一次方程解决问题，请补全他们的分析过程：
第一步：设共有$x$辆车.
第二步：由“若每3人乘一辆车，则余2辆空车”，可得人数为3(x - 2)(用含$x$的代数式表示).
第三步：由“若每2人乘一辆车，则余9人需步行”，可得人数为2x + 9(用含$x$的代数式表示).
第四步：根据两种乘车方式的人数相等，列出方程为3(x - 2) = 2x + 9.

答案： 18.$3(x - 2)$ $2x + 9$ $3(x - 2) = 2x + 9$