《2025年名校课堂七年级数学上册北师大版》

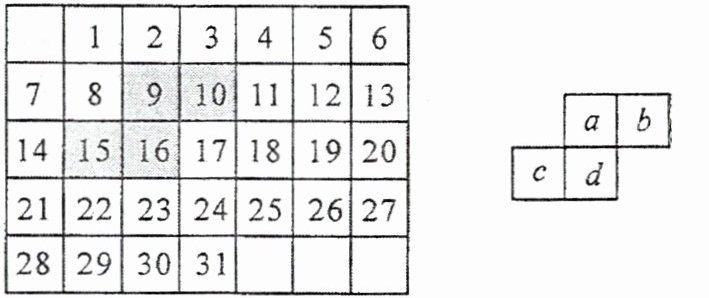
1. 如图，这是某月的月历，用带阴影的方框恰好框住四个数。若这样的阴影方框可以任意移动，且框住这张月历表中的4个数，设$a$表示的数是$x$，则这4个数的和为4x+14。(用含$x$的代数式表示)

答案： 1.4x+14

2. 如图，这是从1开始的连续自然数组成的数表，请观察规律并填空。

(1) 表中第8行的最后一个数是64，它是自然数8的平方，第8行共有15个数。
(2) 第$n$行最后一个数是n^2，第$n$行共有(2n-1)个数。(用含$n$的代数式表示)

答案： $2.(1)64 8 15 (2)n^2 (2n-1)$

3. (2024·云南改编)按一定规律排列的代数式：$2x$，$3x^{2}$，$4x^{3}$，$5x^{4}$，$6x^{5}$，…，第$n$个代数式是(n+1)x^n。

答案： 3.(n+1)x^n

4. (2023·岳阳)观察下列等式：
$1^{2}-1=1×0$；
$2^{2}-2=2×1$；
$3^{2}-3=3×2$；
$4^{2}-4=4×3$；
$5^{2}-5=5×4$；
……
依此规律，则第$n$($n$为正整数)个等式是n^2-n=n(n-1)。

答案： $4.n^2-n=n(n-1)$

5. 观察下面一列数$0$，$3$，$8$，$15$，$24$，…，则它的第10个数是99，第$n$个数是n^2-1(用含正整数$n$的式子表示)。

答案： $5.99 n^2-1$

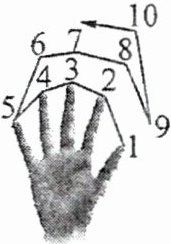
6. 如图，我们做一个游戏：从大拇指开始，按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指……的顺序依次数正整数$1$，$2$，$3$，$4$，$5$，…，当第$n$次数到中指时，恰好数到的数是4n-1(用含$n$的代数式表示)。

答案： 6.4n-1

7. 如图所示，假设有足够多的黑、白棋子按照一定的规律排列成一行，则第2025枚棋子是黑棋。(填“黑棋”或“白棋”)

答案： 7.黑棋

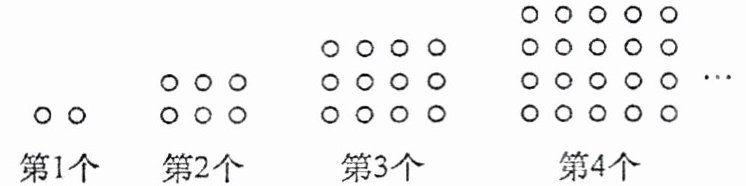
8. (2024·西藏)如图所示的是由若干个大小相同的“○”组成的一组有规律的图案，其中第1个图案用了2个“○”，第2个图案用了6个“○”，第3个图案用了12个“○”，第4个图案用了20个“○”……依照此规律，第$n$个图案中“○”的个数为n(n+1)(用含$n$的代数式表示)。

答案： 8.n(n+1)

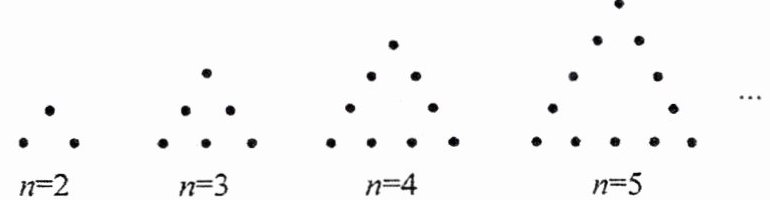
9. 如图，一些点组成形如三角形的图形。如果图形的每条“边”上有$n$($n＞1$)个点(包括两个顶点)，那么当这个图形中点的总数$S=2025$时，$n=$676。

答案： 9.676