《2025年名校课堂七年级数学上册北师大版》

10. 将连续的奇数$1$，$3$，$5$，$7$，$9$，…排成如图所示的数表，小明在数表上圈出了$a$，$b$，$c$，$d$四个数，并求出了它们的和为234。则这4个数在数表中的排列位置可能是(C)

答案： 10.C

11. 下列图形都是由同样大小的棋子按一定的规律排列而成的，其中第1个图形有3颗棋子，第2个图形有9颗棋子，第3个图形有18颗棋子……则第8个图形中棋子的颗数为(B)

A.84
B.108
C.135
D.152

答案： 11.B

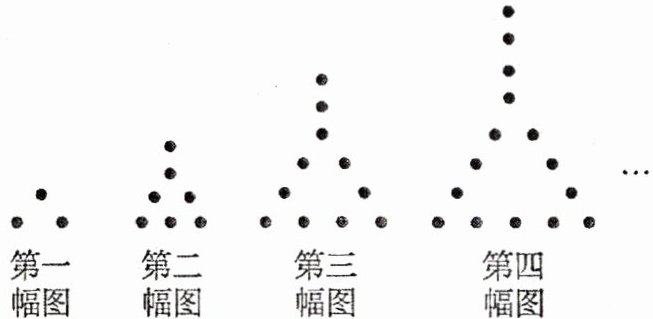
12. 如图，用相同的圆点按照一定的规律拼出图形。第一幅图3个圆点，第二幅图7个圆点，第三幅图11个圆点，第四幅图15个圆点……按照此规律，第$n$幅图形中圆点的个数为(4n-1)。

答案： 12.(4n-1)

13. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个台阶至第4个台阶上依次标着$-5$，$-2$，$1$，$9$，且任意相邻四个台阶上数的和都相等。
尝试 (1) 前4个台阶上数的和是多少？
(2) 第5个台阶上的数$x$是多少？
应用 (3) 求从下到上前31个台阶上数的和。
发现 (4) 试用含$k$（$k$为正整数）的式子表示出数“1”所在的台阶数。

答案： 13.解：
(1)前4个台阶上数的和是-5-2+1+9=3。
(2)由题意，得-2+1+9+x=3，解得x=-5。
(3)由题意知，台阶上的数字是每4个为一循环，
∵31÷4=7⋯⋯3，
∴7×3+1-2-5=15.
∴从下到上前31个台阶上数的和为15。
(4)数“1”所在的台阶数为4k-1(k为正整数)。

14. 新考向 代数推理 如图，下列图形是由一些小正方形和实心圆按一定规律排列而成的，第1个图形中实心圆的个数为$K_{1}=4$，第2个图形中实心圆的个数为$K_{2}=6$……第$n$个图形中实心圆的个数为$K_{n}$。

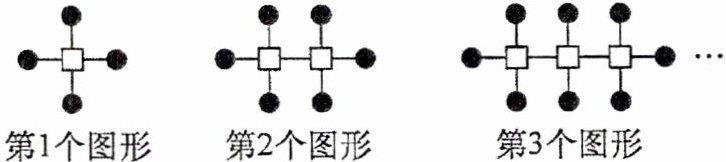
(1) $K_{n}=$2n+2(用含$n$的代数式表示)，$K_{100}=$202。
(2) 我们用“$*$”定义一种新运算：对于任意有理数$a$和正整数$n$，规定$a*n=\frac{a-K_{n}+|a+K_{n}|}{2}$。
例如：$(-3)*2=\frac{-3-K_{2}+|-3+K_{2}|}{2}=\frac{-3-6+|-3+6|}{2}=-3$。
① 求$(-26.6)*10$的值。
② 比较$3*n$与$(-3)*n$的大小。

答案： 14.解：$(1)2n+2 202 (2)①(-26.6)*10= \frac{-26.6-K_{10}+|-26.6+K_{10}|}{2}=\frac{-26.6-22+|-26.6+22|}{2}=-22。$②
∵n是正整数，
∴K_n=2n+2≥4。
∴$\frac{3-K_n+|3+K_n|}{2}=\frac{3-K_n+3+K_n}{2}=3，$$(-3)*n=\frac{-3-K_n+|-3+K_n|}{2}=\frac{-3-K_n-3+K_n}{2}=-3。$
∵3＞-3，
∴3*n＞(-3)*n。