第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 下面四种说法中,正确的是(
A.两点间的连线的长度,叫作两点间的距离
B.连接两点的线段,叫作两点间的距离
C.两点间的距离就是两点间的路程
D.两点间的距离是连接两点的线段的长度
D
)A.两点间的连线的长度,叫作两点间的距离
B.连接两点的线段,叫作两点间的距离
C.两点间的距离就是两点间的路程
D.两点间的距离是连接两点的线段的长度
答案:
1.D
2. (2024·吉林)如图,从长春站去往胜利公园,与其他道路相比,走人民大街路程最近,其蕴含的数学道理是

两点之间线段最短
.
答案:
2.两点之间线段最短
3. 如图,用圆规比较两条线段 $ A'B' $ 和 $ AB $ 的长短,下列结论正确的是(
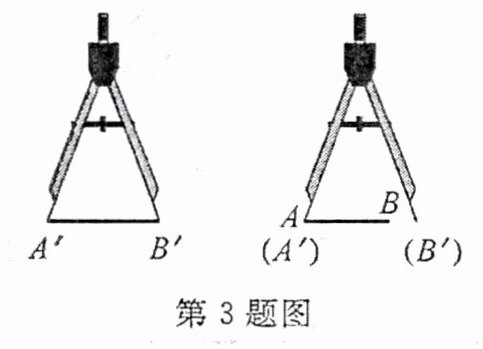
A.$ A'B' > AB $
B.$ A'B' = AB $
C.$ A'B' < AB $
D.不确定
A
)
A.$ A'B' > AB $
B.$ A'B' = AB $
C.$ A'B' < AB $
D.不确定
答案:
3.A
4. 如图,在三角形 $ ABC $ 中,比较线段 $ AC $ 和 $ AB $ 的长短,方法可行的有(
①用刻度尺测量出 $ AB $ 和 $ AC $ 的长度;②用圆规将线段 $ AB $ 叠放到线段 $ AC $ 上,观察点 $ B $ 的位置;③将三角形 $ ABC $ 沿经过点 $ A $ 的直线折叠,使 $ AB $ 和 $ AC $ 重合,观察点 $ B $ 的位置.
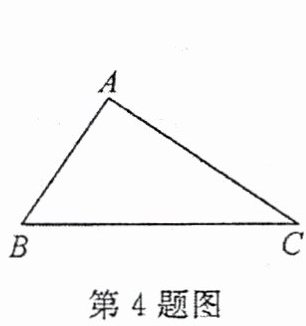
A.0 个
B.1 个
C.2 个
D.3 个
D
)①用刻度尺测量出 $ AB $ 和 $ AC $ 的长度;②用圆规将线段 $ AB $ 叠放到线段 $ AC $ 上,观察点 $ B $ 的位置;③将三角形 $ ABC $ 沿经过点 $ A $ 的直线折叠,使 $ AB $ 和 $ AC $ 重合,观察点 $ B $ 的位置.

A.0 个
B.1 个
C.2 个
D.3 个
答案:
4.D
5. 下列尺规作图的语句正确的是(
A.延长射线 $ AB $ 到点 $ D $
B.以点 $ D $ 为圆心,任意长为半径画弧
C.作直线 $ AB = 3\mathrm{cm} $
D.延长线段 $ AB $ 至点 $ C $,使 $ AC = BC $
B
)A.延长射线 $ AB $ 到点 $ D $
B.以点 $ D $ 为圆心,任意长为半径画弧
C.作直线 $ AB = 3\mathrm{cm} $
D.延长线段 $ AB $ 至点 $ C $,使 $ AC = BC $
答案:
5.B
6. 如图,已知线段 $ a $,借助圆规和直尺作一条线段使它等于 $ 2a $.
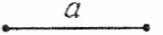
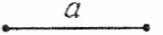
答案:
6.解:如图.①作射线AD;②在AD上依次截取AB=BC=a.则线段AC即为所求.

6.解:如图.①作射线AD;②在AD上依次截取AB=BC=a.则线段AC即为所求.

7. 如图,已知点 $ C $ 在线段 $ AB $ 上,下列条件中不能确定点 $ C $ 是线段 $ AB $ 的中点的是(
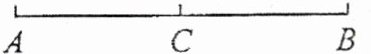
A.$ AC = BC $
B.$ AC + BC = AB $
C.$ AB = 2AC $
D.$ BC = \frac{1}{2}AB $
B
)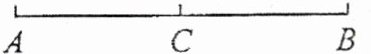
A.$ AC = BC $
B.$ AC + BC = AB $
C.$ AB = 2AC $
D.$ BC = \frac{1}{2}AB $
答案:
7.B
8. 如图,线段 $ AB = 10 $,$ C $ 为线段 $ AD $ 的中点,线段 $ AC = 4.5 $,则线段 $ DB $ 的长为
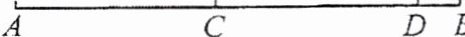
1
.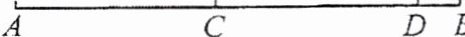
答案:
8.1
9. 如图,$ A $,$ B $,$ C $ 三棵树在同一条直线上,小明正好站在线段 $ AC $ 的中点 $ Q $ 处,$ BC = 2BQ $.

(1) 填空:$ AQ = $
(2) 若 $ BQ = 3\mathrm{m} $,求 $ AC $ 的长.
解:$ \because BQ = 3\mathrm{m} $,$ BC = 2BQ $,
$ \therefore BC = 2BQ = 2 × $
$ \therefore CQ = BC + $
$ \because $ 点 $ Q $ 是 $ AC $ 的中点,
$ \therefore AC = $

(1) 填空:$ AQ = $
CQ
$ = $$\frac{1}{2}$
$ AC $,$ AQ - BC = $BQ
.(2) 若 $ BQ = 3\mathrm{m} $,求 $ AC $ 的长.
解:$ \because BQ = 3\mathrm{m} $,$ BC = 2BQ $,
$ \therefore BC = 2BQ = 2 × $
3
$ = $6
$ (\mathrm{m}) $.$ \therefore CQ = BC + $
BQ
$ = 6 + $3
$ = $9
$ (\mathrm{m}) $.$ \because $ 点 $ Q $ 是 $ AC $ 的中点,
$ \therefore AC = $
2
$ CQ = $18
$ \mathrm{m} $.
答案:
9.
(1)CQ $\frac{1}{2}$ BQ
(2)3 6 BQ 3 9 2 18
(1)CQ $\frac{1}{2}$ BQ
(2)3 6 BQ 3 9 2 18
查看更多完整答案,请扫码查看


