《2025年名校课堂七年级数学上册北师大版》

11. 已知 $A = 2x^{2} + xy - 3y - 1,B = x^{2} - xy$.
(1)求 $A - 2B$.
(2)若 $A - 2B$ 的值与 $y$ 的值无关，求 $x$ 的值.

答案： 11.
(1)$\because A = 2x^2 + xy - 3y - 1$，$B = x^2 - xy$，$\therefore A - 2B = 2x^2 + xy - 3y - 1 - 2(x^2 - xy) = 3xy - 3y - 1$。
(2)由
(1)知，$A - 2B = 3xy - 3y - 1 = y(3x - 3) - 1$。$\because A - 2B$的值与y的值无关，$\therefore 3x - 3 = 0$，解得$x = 1$。

12. (2024·宿州埇桥区期中)某商场销售一种微波炉和电磁炉，微波炉每台定价 800 元，电磁炉每台定价 200 元. “双十一”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：买一台微波炉送一台电磁炉；
方案二：微波炉和电磁炉都按定价的 $90\%$ 付款.
现某客户要到该商场购买 2 台微波炉、$x(x ＞ 2)$ 台电磁炉.
(1)若该客户按方案一购买，需付款200x + 1200元；若该客户按方案二购买，需付款180x + 1440元. (用含 $x$ 的代数式表示)
(2)当 $x = 5$ 时，通过计算说明此时按哪种方案购买较为合算.

答案： 12.
(1)$(200x + 1200)$（$180x + 1440$）
(2)当$x = 5$时，方案一：$200 × 5 + 1200 = 2200$（元）；方案二：$180 × 5 + 1440 = 2340$（元）。因为$2200 ＜ 2340$，所以按方案一购买较为合算。

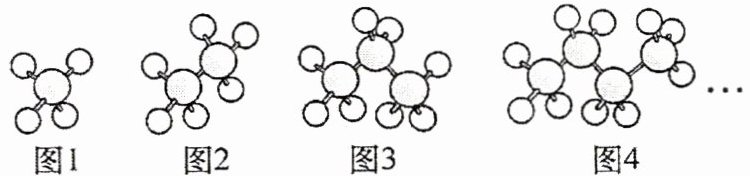
13. 新考向 跨学科 (2024·重庆)烷烃是一类由碳、氢元素组成的有机化合物质，如图所示的是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子. 第 1 种如图 1 有 4 个氢原子，第 2 种如图 2 有 6 个氢原子，第 3 种如图 3 有 8 个氢原子，……按照这一规律，第 10 种化合物的分子结构模型中氢原子的个数是(B)


A.20
B.22
C.24
D.26

答案： 13.B

14. (2024·宿州埇桥区期中)观察一列单项式：$x,-3x^{3},7x^{5},-15x^{7},31x^{9},\cdots$，则第 $n$ 个单项式是(C)

A.$(-1)^{n + 1}(2n - 1)x^{2n - 1}$
B.$(-1)^{n}(2^{n} - 1)x^{2n + 1}$
C.$(-1)^{n + 1}(2^{n} - 1)x^{2n - 1}$
D.$(-1)^{n}(2^{n} + 1)x^{2n - 1}$

答案： 14.C

15. 如图，下列各图形中的三个数之间均具有相同的规律，依此规律，那么第 4 个图形中的 $x =$63；一般地，用含 $m,n$ 的代数式表示 $y$，那么 $y =$m(n + 1).

答案： 15.63 $m(n + 1)$

16. 新考向 代数推理 “歌唱家在家唱歌”“蜜蜂酿蜂蜜”这两句话从左往右读和从右往左读，结果完全相同，文学上把这样的现象称为“回文”. 数学上也有类似的“回文数”，比如 252，7 887，34 143. 小明在计算两位数减法的过程中意外地发现，有些等式从左往右读的结果和从右往左读的结果一样，例如：$65 - 38 = 83 - 56$；$91 - 37 = 73 - 19$；$54 - 36 = 63 - 45$. 数学上把这类等式叫作“减法回文等式”.
(1)观察以上等式，请再写出一个“减法回文等式”.
(2)请归纳“减法回文等式”的被减数 $\overline{ab}$ (十位数字为 $a$，个位数字为 $b$) 与减数 $\overline{cd}$ 应满足的条件，并说明理由.

答案： 16.
(1)$81 - 72 = 27 - 18$（答案不唯一）。
(2)“减法回文等式”的被减数$\overline{ab}$（十位数字为a，个位数字为b）与减数$\overline{cd}$应满足的条件是$a - c = d - b$。$\because 10a + b - (10c + d) = 10d + c - (10b + a)$，$\therefore 10a + b - 10c - d = 10d + c - 10b - a$。$\therefore 11a + 11b - 11c - 11d = 0$。$\therefore 11(a - c) = 11(d - b)$。$\therefore a - c = d - b$。